Geometric Sequences and Series

Geometric Sequences

A geometric sequence is an ordered list of numbers in which each term after the first is found by multiplying the previous one by a constant called

r

, the common ratio.

Learning Objectives

Calculate the

n

th term of a geometric sequence given the initial value

a

and common ratio

r

Key Takeaways

Key Points

The general form of a geometric sequence is: $a, ar, ar^2, ar^3, ar^4, \cdots$
The $n$ th term of a geometric sequence with initial value $n$ and common ratio $r$ is given by: ${ a }_{ n }=a{ r }^{ n-1 }$ .

Key Terms

geometric sequence: An ordered list of numbers in which each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. Also known as a geometric progression.

Definition of Geometric Sequences

A geometric progression, also known as a geometric sequence, is an ordered list of numbers in which each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio

r

. For example, the sequence

2, 6, 18, 54, \cdots

is a geometric progression with common ratio

3

. Similarly

10,5,2.5,1.25,\cdots

is a geometric sequence with common ratio

\displaystyle{\frac{1}{2}}

. Thus, the general form of a geometric sequence is:

a, ar, ar^2, ar^3, ar^4, \cdots

The

n

th term of a geometric sequence with initial value

a

and common ratio

r

is given by

{ a }_{ n }=a{ r }^{ n-1 }

Such a geometric sequence also follows the recursive relation:

a_n=ra_{n-1}

for every integer

n\ge 1.

Behavior of Geometric Sequences

Generally, to check whether a given sequence is geometric, one simply checks whether successive entries in the sequence all have the same ratio. The common ratio of a geometric series may be negative, resulting in an alternating sequence. An alternating sequence will have numbers that switch back and forth between positive and negative signs. For instance:

1,-3,9,-27,81,-243, \cdots

is a geometric sequence with common ratio

-3

. The behavior of a geometric sequence depends on the value of the common ratio. If the common ratio is:

Positive, the terms will all be the same sign as the initial term
Negative, the terms will alternate between positive and negative
Greater than $1$ , there will be exponential growth towards positive infinity ( $+\infty$ )
$1$ , the progression will be a constant sequence
Between $-1$ and $1$ but not $0$ , there will be exponential decay toward $0$
$-1$ , the progression is an alternating sequence (see alternating series)
Less than $-1$ , for the absolute values there is exponential growth toward positive and negative infinity (due to the alternating sign)

Geometric sequences (with common ratio not equal to

-1

1

0

) show exponential growth or exponential decay, as opposed to the linear growth (or decline) of an arithmetic progression such as

4, 15, 26, 37, 48, \cdots

(with common difference

11

). This result was taken by T.R. Malthus as the mathematical foundation of his Principle of Population. Note that the two kinds of progression are related: exponentiating each term of an arithmetic progression yields a geometric progression, while taking the logarithm of each term in a geometric progression with a positive common ratio yields an arithmetic progression. An interesting result of the definition of a geometric progression is that for any value of the common ratio, any three consecutive terms

a

b

, and

c

will satisfy the following equation:

{b}^{2}=ac

Summing the First n Terms in a Geometric Sequence

By utilizing the common ratio and the first term of a geometric sequence, we can sum its terms.

Learning Objectives

Calculate the sum of the first

n

terms in a geometric sequence

Key Takeaways

Key Points

The terms of a geometric series form a geometric progression, meaning that the ratio of successive terms in the series is constant.
The general form of an infinite geometric series is: $\displaystyle{\sum _{ n=0 }^{ \infty }{ { z }^{ n } }}$ . The behavior of the terms depends on the common ratio $r$ .
For $r\neq 1$ , the sum of the first $n$ terms of a geometric series is given by the formula $\displaystyle{s = a\frac { 1-{ r }^{ n } }{ 1-r } }$ .

Key Terms

geometric series: An infinite sequence of numbers to be added, whose terms are found by multiplying the previous term by a fixed, non-zero number called the common ratio.
geometric progression: A series of numbers in which each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.

Geometric series are examples of infinite series with finite sums, although not all of them have this property. Historically, geometric series played an important role in the early development of calculus, and they continue to be central in the study of the convergence of series. Geometric series are used throughout mathematics, and they have important applications in physics, engineering, biology, economics, computer science, queueing theory, and finance. The terms of a geometric series form a geometric progression, meaning that the ratio of successive terms in the series is constant. For example, the following series:

\displaystyle{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+ \cdots=\sum _{ n=0 }^{ \infty }{ \frac { 1 }{ { 2 }^{ n } } }}

is geometric, because each successive term can be obtained by multiplying the previous term by

\displaystyle{\frac{1}{2}}

. The general form of an infinite geometric series is:

\displaystyle{\sum _{ n=0 }^{ \infty }{ { z }^{ n } }}

It is possible to visualize this concept with a diagram:

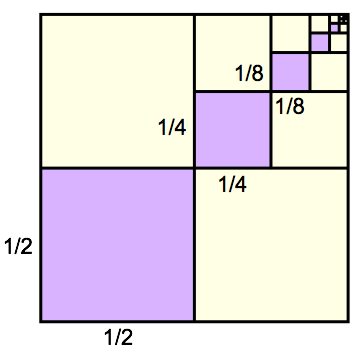A square with a purple square in the lower left quadrant, occupying a quarter of the original volume and with side lengths half the original side length. The upper right quadrant has a purple square in its lower left quadrant, side lengths 1/4 the original. These increasingly small purple squares with sides half the length each time continue to infinity, creating a diagonal line of shrinking squares from the lower left to upper right of the original square.

Infinite geometric series: Each of the purple squares is obtained by multiplying the area of the next larger square by

\displaystyle{\frac{1}{4}}

. The area of the first square is

\displaystyle{\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}}

, and the area of the second square is

\displaystyle{\frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16}}

The following are several geometric series with different common ratios. The behavior of the terms depends on the common ratio

r

$4+40+400+4000+\dots$ has the common ratio $10$
$\displaystyle{9+3+1+\frac{1}{3}+\frac{1}{9}+\dots}$ has the common ratio ${\frac{1}{3}}$
$3+3+3+3+\dots$ has the common ratio $1$
$\displaystyle{1-\frac{1}{2}+\frac{1}{4} -\frac{1}{8}+\dots}$ has the common ratio $-\frac{1}{2}$
$3-3+3-3+\dots$ has the common ratio $-1$

The value of

r

provides information about the nature of the series:

If $r$ is between $-1$ and $+1$ , the terms of the series become smaller and smaller, approaching zero in the limit, and the series converges to a sum. Consider a sequence where $r$ is one-half ${\left(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \cdots \right)}$ , which has a sum of one.
If $r$ is greater than $1$ or less than $-1$ , the terms of the series become larger and larger in magnitude. The sum of the terms also gets larger and larger, and the series has no sum. The series diverges.
If $r$ is equal to $1$ , all of the terms of the series are the same. The series diverges.
If $r$ is $-1$ , the terms take two values alternately $\left(\text{e.g.}, 2,-2,2,-2,2,-2,\cdots \right)$ . The sum of the terms oscillates between two values $\left(\text{e.g.}, 2,0,2,0,2,0,\cdots \right)$ . This is a different type of divergence and again the series has no sum.

We can use a formula to find the sum of a finite number of terms in a sequence. For

r\neq 1

, the sum of the first

n

terms of a geometric series is:

\displaystyle{ \begin{align} s &= {a+ar+a{ r }^{ 2 }+a{ r }^{ 3 }+\cdots +a{ r }^{ n-1 } } \\ &=\sum _{ k=0 }^{ n-1 }{ a{ r }^{ k } } \\ &= a\frac { 1-{ r }^{ n } }{ 1-r } \end{align} }

where

a

is the first term of the series, and

r

is the common ratio. Therefore, by utilizing the common ratio and the first term of the sequence, we can sum the first

n

terms.

Example

Find the sum of the first five terms of the geometric sequence

\left(6, 18, 54, 162, \cdots \right)

. In this case,

a=6

and

n=5

. Also, note that

r = 3

, because each term is multiplied by a factor of

3

to find the subsequent term. Substituting these values into the sum formula, we have:

\displaystyle{ \begin{align} s &= a\frac { 1-{ r }^{ n } }{ 1-r } \\ &= 6\cdot\frac { 1-{ 3 }^{ 5 } }{ 1-3 } \\ &= 6\cdot\frac {{ -242 } }{ -2 } \\ &= 6 \cdot 121 \\ &= 726 \end{align} }

Infinite Geometric Series

Geometric series are one of the simplest examples of infinite series with finite sums.

Learning Objectives

Calculate the sum of an infinite geometric series and recognize when a geometric series will converge

Key Takeaways

Key Points

The sum of a geometric series is finite as long as the terms approach zero; as the numbers near zero, they become insignificantly small, allowing a sum to be calculated despite the series being infinite.
For an infinite geometric series that converges, its sum can be calculated with the formula $\displaystyle{s = \frac{a}{1-r}}$ .

Key Terms

converge: Approach a finite sum.
geometric series: An infinite sequence of summed numbers, whose terms change progressively with a common ratio.

A geometric series is an infinite series whose terms are in a geometric progression, or whose successive terms have a common ratio. If the terms of a geometric series approach zero, the sum of its terms will be finite. As the numbers near zero, they become insignificantly small, allowing a sum to be calculated despite the series being infinite. A geometric series with a finite sum is said to converge. A series converges if and only if the absolute value of the common ratio is less than one:

\left | r \right | < 1

What follows in an example of an infinite series with a finite sum. We will calculate the sum

s

of the following series:

\displaystyle{s = 1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +\frac { 8 }{ 27 } + \cdots}

This series has common ratio

\displaystyle{\frac{2}{3}}

. If we multiply through by this common ratio, then the initial term

1

becomes

\displaystyle{\frac{2}{3}}

, the

\displaystyle{\frac{2}{3}}

becomes

\displaystyle{\frac{4}{9}}

, and so on:

\displaystyle{\frac{2}{3} s = \frac { 2 }{ 3 } +\frac { 4 }{ 9 } +\frac { 8 }{ 27 } +\frac { 16 }{ 81 } + \cdots}

This new series is the same as the original, except that the first term is missing. Subtracting the new series

\displaystyle{\frac{2}{3}s}

from the original series,

s

cancels every term in the original but the first:

\displaystyle{ \begin{align} s-\frac{2}{3}s &=1 \\ \therefore s &= 3 \end{align} }

A similar technique can be used to evaluate any self-similar expression. A formula can be derived to calculate the sum of the terms of a convergent series. The formula used to sum the first

n

terms of any geometric series where

r\neq 1

is:

\displaystyle s= a\frac { 1-{ r }^{ n } }{ 1-r }

If a series converges, we want to find the sum of not only a finite number of terms, but all of them. If

\left | r \right | <1

, then we see that as

n

becomes very large,

r^n

becomes very small. We express this by writing that as

n\rightarrow \infty

(as

n

approaches infinity),

r^n\rightarrow 0

. Applying

r^n\rightarrow 0

, we can find a new formula for the sum of an infinitely long geometric series:

\displaystyle{ \begin{align} s &= a\frac{1-r^n}{1-r} \\ &\rightarrow a\frac{1}{1-r} \quad \text{as } r^n\rightarrow 0\\ &= \frac{a}{1-r} \end{align} }

Therefore, for

|r|<1

, we can write the infinite sum as:

\displaystyle{s = \frac{a}{1-r}}

Example

Find the sum of the infinite geometric series

64+ 32 + 16 + 8 + \cdots

First, find

r

, or the constant ratio between each term and the one that precedes it:

\displaystyle{ \begin{align} r &= \frac{32}{64} \\ &= \frac{1}{2} \end{align} }

Substitute

a=64

and

\displaystyle r= \frac{1}{2}

into the formula for the sum of an infinite geometric series:

\displaystyle{ \begin{align} s &= \frac{64}{1-\frac{1}{2}} \\ &= \frac{64}{\frac{1}{2}} \\ &= 128 \end{align} }

Applications of Geometric Series

Geometric series have applications in math and science and are one of the simplest examples of infinite series with finite sums.

Learning Objectives

Apply geometric sequences and series to different physical and mathematical topics

Key Takeaways

Key Points

A repeating decimal can be viewed as a geometric series whose common ratio is a power of $\displaystyle{\frac{1}{10}}$ .
Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line.
The interior of the Koch snowflake is a union of infinitely many triangles. In the study of fractals, geometric series often arise as the perimeter, area, or volume of a self-similar figure.
Knowledge of infinite series allows us to solve ancient problems, such as Zeno's paradoxes.

Key Terms

geometric series: An infinite sequence of summed numbers, whose terms change progressively with a common ratio.
fractal: A natural phenomenon or mathematical set that exhibits a repeating pattern that can be seen at every scale.

Geometric series played an important role in the early development of calculus, and continue as a central part of the study of the convergence of series. Geometric series are used throughout mathematics. They have important applications in physics, engineering, biology, economics, computer science, queueing theory, and finance. Geometric series are one of the simplest examples of infinite series with finite sums, although not all of them have this property.

Repeating Decimal

A repeating decimal can be thought of as a geometric series whose common ratio is a power of

\displaystyle{\frac{1}{10}}

. For example:

\displaystyle{0.7777 \cdots = \frac{7}{10} + \frac{7}{100}+ \frac{7}{1000}+ \frac{7}{10000}+ \cdots}

The formula for the sum of a geometric series can be used to convert the decimal to a fraction:

\displaystyle{ \begin{align} 0.7777 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{ 7 }{ 10 } }{ 1-\frac{ 1 }{ 10 } } \\ &= \frac{\left(\frac{7}{10}\right)}{\left(\frac{9}{10}\right)} \\ &= \left(\frac{7}{10}\right)\left(\frac{10}{9}\right)\\ &= \frac { 7 }{ 9 } \end{align} }

The formula works for any repeating term. Some more examples are:

\displaystyle{ \begin{align} 0.123412341234 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{1234}{ 10000 } }{ 1-\frac{ 1 }{ 10000 } } \\ &= \frac{\left(\frac{1234}{ 10000 }\right)}{\left(\frac{9999}{10000}\right)} \\ &= \left(\frac{1234}{ 10000 }\right)\left(\frac{10000}{9999}\right)\\ &= \frac { 1234 }{ 9999 } \end{align} }

\displaystyle{ \begin{align} 0.0909090909 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{9}{ 100 } }{ 1-\frac{ 1 }{ 100 } } \\ &= \frac{\left(\frac{9}{ 100 }\right)}{\left(\frac{99}{100}\right)} \\ &= \left(\frac{9}{100}\right)\left(\frac{100}{99}\right)\\ &= \frac { 9 }{ 99 } \\ &= \frac{1}{11} \end{align} }

\displaystyle{ \begin{align} 0.143814381438 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{1438}{ 10000 } }{ 1-\frac{ 1 }{ 10000 } } \\ &= \frac{\left(\frac{1438}{ 10000 }\right)}{\left(\frac{9999}{10000}\right)} \\ &= \left(\frac{1438}{ 10000 }\right)\left(\frac{10000}{9999}\right)\\ &= \frac { 1438 }{ 9999 } \end{align} }

\displaystyle{ \begin{align} 0.9999 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{ 9 }{ 10 } }{ 1-\frac{ 1 }{ 10 } } \\ &= \frac{\left(\frac{9}{10}\right)}{\left(\frac{9}{10}\right)} \\ &= \left(\frac{9}{10}\right)\left(\frac{10}{9}\right)\\ &= \frac { 9 }{ 9 } \\ &= 1 \end{align} }

That is, a repeating decimal with a repeating part of length

n

is equal to the quotient of the repeating part (as an integer) and

10^n - 1

Archimedes' Quadrature of the Parabola

Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. His method was to dissect the area into an infinite number of triangles.

A line intersecting a parabola is formed into a blue triangle by placing one vertex on the inside of the parabola between the points of intersection, which are the other two vertices. There are now two lines intersecting the parabola, which are formed into green triangles in a similar way, The sides of these triangles are used to form 4 yellow triangles, then those to form 8 red triangles, on to infinity.

Archimedes' Theorem: Archimedes' dissection of a parabolic segment into infinitely many triangles.

Archimedes' Theorem states that the total area under the parabola is $\displaystyle{\frac{4}{3}}$ of the area of the blue triangle. He determined that each green triangle has $\displaystyle{\frac{1}{8}}$ the area of the blue triangle, each yellow triangle has $\displaystyle{\frac{1}{8}}$ the area of a green triangle, and so forth. Assuming that the blue triangle has area $1$ , the total area is an infinite series:

\displaystyle{1+2 \left ( \frac { 1 }{ 8 } \right ) +4 { \left ( \frac { 1 }{ 8 } \right ) }^{ 2 }+8{ \left ( \frac { 1 }{ 8 } \right ) }^{ 3 }+ \cdots}

The first term represents the area of the blue triangle, the second term the areas of the two green triangles, the third term the areas of the four yellow triangles, and so on. Simplifying the fractions gives:

\displaystyle{1+ \frac{1}{4}+ \frac{1}{16}+ \frac{1}{64}+ \cdots}

This is a geometric series with common ratio

\displaystyle{\frac{1}{4}}

, and the fractional part is equal to

\displaystyle{\frac{1}{3}}

Fractal Geometry

Koch snowflake: The interior of a Koch snowflake is comprised of an infinite amount of triangles.

The Koch snowflake is a fractal shape with an interior comprised of an infinite amount of triangles. In the study of fractals, geometric series often arise as the perimeter, area, or volume of a self-similar figure. In the case of the Koch snowflake, its area can be described with a geometric series.

The original shape is a triangle. The first iteration adds equilateral triangles to the outsides of the triangle on the middle third of each side. The second iteration adds equilateral triangles to the outsides of each of the six points in the new shape, on the middle thirds of these. These iterations continue to infinity, with an equilateral triangle a third of the side length being added to any free side in each iteration.

Constructing the Koch snowflake: the first four iterations: Each iteration adds a set of triangles to the outside of the shape.

The area inside the Koch snowflake can be described as the union of an infinite number of equilateral triangles. In the diagram above, the triangles added in the second iteration are exactly $\displaystyle{\frac{1}{3}}$ the size of a side of the largest triangle, and therefore they have exactly $\displaystyle{\frac{1}{9}}$ the area. Similarly, each triangle added in the second iteration has $\displaystyle{\frac{1}{9}}$ the area of the triangles added in the previous iteration, and so forth. Taking the first triangle as a unit of area, the total area of the snowflake is:

\displaystyle{1+3 \left ( \frac { 1 }{ 9 } \right ) +12{ \left ( \frac { 1 }{ 9 } \right ) }^{ 2 }+48{ \left ( \frac { 1 }{ 9 } \right ) }^{ 3 }+ \cdots}

The first term of this series represents the area of the first triangle, the second term the total area of the three triangles added in the second iteration, the third term the total area of the twelve triangles added in the third iteration, and so forth. Excluding the initial term

1

, this series is geometric with constant ratio

\displaystyle{r = \frac{4}{9}}

. The first term of the geometric series is

\displaystyle{a = 3 \frac{1}{9} = \frac{1}{3}}

, so the sum is:

\displaystyle{ \begin{align} 1+ \frac { a }{ 1-r } &=1+ \frac { \frac{1}{3} }{ 1- \frac{4}{9} } \\ &= \frac{8}{5} \end{align} }

Thus the Koch snowflake has

\displaystyle{\frac{8}{5}}

of the area of the base triangle.

Zeno's Paradoxes

Zeno's Paradoxes are a set of philosophical problems devised by an ancient Greek philosopher to support the doctrine that the truth is contrary to one's senses. Simply stated, one of Zeno's paradoxes says: There is a point, A, that wants to move to another point, B. If A only moves half of the distance between it and point B at a time, it will never get there, because you can continue to divide the remaining space in half forever. Zeno's mistake is in the assumption that the sum of an infinite number of finite steps cannot be finite. We now know that his paradox is not true, as evidenced by the convergence of the geometric series with

\displaystyle{r = \frac{1}{2}}

. This problem has been solved by modern mathematics, which can apply the concept of infinite series to find a sum of the distances traveled.

Geometric Sequences and Series