Systems of Three Equations in Three Variables
6.2 Learning Objectives
- Introduction to systems in three variables
- Define the solution to a system of three equations in three variables
- Determine whether an ordered triple is a solution to a system
- Solve a systems of equations in three variables using elimination and back-substitution
- CLassify solutions to sustems in three variables
- Identify an inconsistent system of equations in three variables
- Identify a dependent system of equations in three variables
- Applications of systems in three variables
- Write a system of three equations with three unknowns given a business scenario
- Solve the system you define
Solution Set, One Solution
The figure below illustrates how a system with three variables can have one solution. Systems that have a single solution are those which result in a solution set consisting of an ordered triple [latex]\left(x,y,z\right)[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.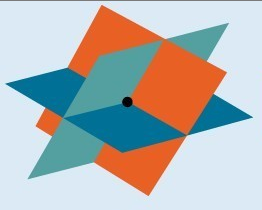
Example 6.2.A
Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.Answer: We will check each equation by substituting in the values of the ordered triple for [latex]x,y[/latex], and [latex]z[/latex]. [latex-display]\begin{array}{ccccc}\begin{array}{r}\hfill x+y+z=2\\ \hfill \left(3\right)+\left(-2\right)+\left(1\right)=2\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill \text{}6x - 4y+5z=31\\ \hfill 6\left(3\right)-4\left(-2\right)+5\left(1\right)=31\\ \hfill 18+8+5=31\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill \text{}5x+2y+2z=13\\ \hfill 5\left(3\right)+2\left(-2\right)+2\left(1\right)=13\\ \hfill \text{}15 - 4+2=13\\ \hfill \text{True}\end{array}\end{array}[/latex-display] The ordered triple [latex]\left(3,-2,1\right)[/latex] is indeed a solution to the system.
How To: Given a linear system of three equations, solve for three unknowns.
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Example 6.2.B
Solve the system [latex-display]\displaystyle\begin{cases}x-\frac{1}{3}y+\frac{1}{2}z=1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y-\frac{1}{2}z=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,z=-1\end{cases}[/latex-display]Answer: The third equation states that z = −1, so we substitute this into the second equation to obtain a solution for y. [latex-display]\begin{array}{ccc}y-\frac{1}{2}(-1)=4\\y+\frac{1}{2}=4\\y=4-\frac{1}{2}\\y=\frac{8}{2}-\frac{1}{2}\\y=\frac{7}{2}\end{array}[/latex-display] Now we have two of our solutions and we can substitute them both into the first equation to solve for x. [latex-display]\begin{array}{ccc}x-\frac{1}{3}\left(\frac{7}{2}\right)+\frac{1}{2}\left(-1\right)=1\\x-\frac{7}{6}-\frac{1}{2}=1\\x-\frac{7}{6}-\frac{3}{6}=1\\x-\frac{10}{6}=1\\x=1+\frac{10}{6}\\x=\frac{6}{6}+\frac{10}{6}\\x=\frac{16}{6}=\frac{8}{3}\end{array}[/latex-display] Now we have our ordered triple, remember that where you place the solutions matters!
Answer
[latex-display](x,y,z)=\left(\frac{8}{3},\frac{7}{2},-1\right)[/latex-display]Analysis of the solution:
Each of the lines in this system represents a plane (think about a sheet of paper). If you imagine three sheets of notebook paper each representing a portion of these planes, you will start to see the complexities involved in how three such planes can intersect. Below is a sketch of the three planes. It turns out that any two of these planes intersect in a line, so our intersection point is where all three of these lines meet.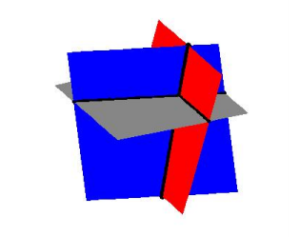 Three Planes Intersecting.
Three Planes Intersecting.Example 6.2.C
Find a solution to the following system:Answer:
[latex]\begin{array}{rrr}-2y+(6)=6\\-2y=6-6\\-2y=0\\\,\,\,\,y=0\end{array}[/latex]
Be careful here not to get confused with a solution of y = 0 and an inconsistent solution. It's ok for variables to equal 0. Now we can substitute z = 6 and y = 0 back into the original equation.[latex]\begin{array}{rrr}x-y+z=5\\x-0+6=5\\x+6=5\\x=5-6\\x=-1\end{array}[/latex]
Answer
[latex-display](x,y,z)=(-1,0,6)[/latex-display]6.2.1 Classify solutions to systems in three variables
Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a false statement, such as [latex]3=7[/latex] or some other contradiction.Infinitely Many or No Solutions
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space. The graphic below shows how three planes can intersect to form a line giving the system infinitely many solutions.
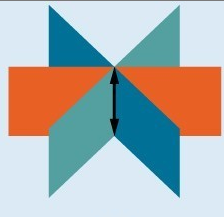 Infinitely many solutions.
Infinitely many solutions.- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common. Three parallel planes (c), two parallel planes and one intersecting plane (b), three planes that intersect the other two but not at the same location (a).
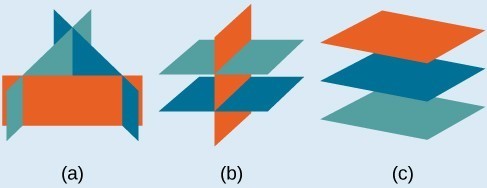
Example 6.2.D
Solve the following system.[latex]\begin{array}{ll}\text{ }x - 3y+z=4\,\,\,\,\,\,\,\,\,\,\,\,\left(1\right)\\ \,\,\,\,\,\,-y-4z=7\,\,\,\,\,\,\,\,\,\,\,\,\,\left(2\right)\,\,\,\,\\\,\,\,\,\,\,\,\,2y+8z=-12\,\,\,\,\,\,\,(3)\end{array}[/latex]
Answer: If you multiply equation (2) by 2 and add (2) and (3) together, you can eliminate y and solve for z. First, multiply equation (2) by 2.
[latex]\begin{array}\,\,\,\,\,\,2(-y-4z=7)\\-2y-8z=14\end{array}[/latex]
Next, add equations (2) and (3) together to eliminate y and solve for z.
[latex]\begin{array}\,\,\,\,\,\,-2y-8z=14\\\underline{+2y+8z=-12}\\0+0=2\\0=2\end{array}[/latex]
Recall that when we were solving systems with two variables, a non-true solution such as [latex]0=2[/latex] implied that there was no solution to the system.
This can happen with a system of three variables as well.
Answer
No solution, or DNEExample 6.2.E
Find the solution to the given system of three equations in three variables.[latex]\begin{array}{rr}\hfill \text{ }2x+y - 3z=0& \hfill \left(1\right)\\ \hfill 4x+2y - 6z=0& \hfill \left(2\right)\\ \hfill \text{ }x-y+z=0& \hfill \left(3\right)\end{array}[/latex]
Answer: First, we can multiply equation (1) by [latex]-2[/latex] and add it to equation (2).
[latex]\begin{array} −4x−2y+6z=0 \hfill& \text{equation }\left(1\right)\text{multiplied by }−2 \\ 4x+2y−6z=0\hfill&\left(2\right) \end{array}[/latex]
We do not need to proceed any further. The result we get is an identity, [latex]0=0[/latex], which tells us that this system has an infinite number of solutions. As shown in the figure below, two of the planes are the same and they intersect the third plane on a line. The solution set is infinite, as all points along the intersection line will satisfy all three equations.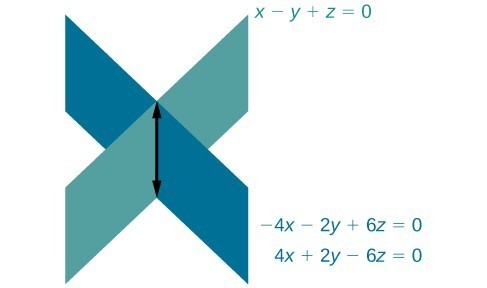
Answer
There are an infinite number of solutions.6.2.2 Applications
Systems can be helpful for solving real-world problems. In this example, we will write three equations that model sales at an art fair to learn how many prints should be sold to break even for the cost of the booth rental.Example 6.2.F
Andrea sells photographs at art fairs. She prices the photos according to size: small photos cost $10, medium photos cost $15, and large photos cost $40. She usually sells as many small photos as medium and large photos combined. She also sells twice as many medium photos as large. A booth at the art fair costs $300. If her sales go as usual, how many of each size photo must she sell to pay for the booth?Answer: To set up the system, first choose the variables. In this case the unknown values are the number of small, medium, and large photos. S = number of small photos sold M = number of medium photos sold L = number of large photos sold The total of her sales must be $300 to pay for the booth. We can find the total by multiplying the cost for each size by the number of that size sold. 10S = money received for small photos 15M = money received for medium photos 40L = money received for large photos
Total Sales: 10S + 15M + 40L = 300
The number of small photos is the same as the total of medium and large photos combined.S = M + L
She sells twice as many medium photos as large photos.M = 2L
To make things easier, rewrite the equations to be in the same format, with all variables on the left side of the equal sign and only a constant number on the right.[latex]\begin{cases}10S+15M+40L=300\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,S–M–L=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M–2L=0\end{cases}[/latex]
Now solve the system. Step 1: First choose two equations and eliminate a variable. Since one equation has no S variable, it may be helpful to use the other two equations and eliminate the S variable from them. Multiply the second equation by −10 and add.[latex]\begin{array}-10(S–M–L=0)\\-10s+10M+10L=0\end{array}[/latex]
[latex]\begin{array}{ccc}10S+15M+40L=300\\\underline{+(-10s+10M+10L=0)}\\25M+50L=300\end{array}[/latex]
Step 2: The second equation for our two-variable system will be the remaining equation (that has no S variable). Eliminate a second variable using the equations from steps 1 and 2. While you could multiply the second equation by 25 to eliminate L, the numbers will stay nicer if you divide the first equation by 25. Don’t forget to be careful of the signs! Divide first:[latex]\begin{array}{ccc}\frac{25}{25}M+\frac{50}{25}L=\frac{300}{25}\\M+2L=12\end{array}[/latex]
Now eliminate L by adding M-2L=0 to this new equation.[latex]\begin{array}{ccc}M+2L=12\\\underline{+(M–2L=0)}\\2M=12\\M=\frac{12}{2}=6\end{array}[/latex]
Step 3: Use M=6 and one of the equations containing just two variables to solve for the second variable. It’s best to use one of the original equations—in case an error was made in multiplication.[latex]\begin{array}{ccc}M=2L\\6=2L\\3=L\end{array}[/latex]
Step 4: Use the two found values and one of the original equations to solve for the third variable.
[latex]\begin{array}{ccc}S–M–L=0\\S-6-3=0\\S-9=0\\s=9\end{array}[/latex]
Step 5: Check your answer. With application problems, it’s sometimes easier (and better) to use the original wording of the problem rather than the equations you write.
She usually sells as many small photos as medium and large photos combined.- Medium and large photos combined =6 + 3 = 9, which is the number of small photos.
- Medium photos is 6, which is twice the number of large photos (3).
- Andrea receives $10(9) or $90 for the 9 small photos, $15(6) or $90 for the 6 medium photos, and $40(3) or $120 for the large photos. $90 + $90 + $120 = $300.
Answer
If Andrea sells 9 small photos, 6 medium photos, and 3 large photos, she’ll receive exactly the amount of money needed to pay for the booth.In the following video example we show how to define a system of three equations in three variables that represents a mixture needed by a chemist.
https://youtu.be/612Ad0W9ZeY Our last example shows you how to write a system of three equations that represents ticket sales for a theater that has three different prices for tickets. https://youtu.be/Wg_v5R7BFo0Summary
- The solution to a system of linear equations in three variables is an ordered triple in the form [latex](x,y,z)[/latex]
- Solutions can be verified using substitution and the order of operations
- Systems of three variables can be solved using the same techniques as we used to solve systems with two variables, including elimination and substitution.
- A system with three variables can have one, none, or many solutions
- A system with no solutions will have a non-true result when solving
- A system with many solutions will have an identity result when solving
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra: 8.1 Systems of Linear Equations: Gaussian Elimination. Authored by: Stitz, Carl and Zeager, Jeff. Located at: https://www.stitz-zeager.com/szca07042013.pdf. License: CC BY: Attribution.
- Ex: Solve a System of 3 Equations with 3 Unknowns Using Back Substitution. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 2: System of Three Equations with Three Unknowns Using Elimination. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 1: System of Three Equations with Three Unknowns Using Elimination. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 4: System of Three Equations with Three Unknowns Using Elimination (No Solution). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 5: System of Three Equations with Three Unknowns Using Elimination (Infinite Solutions). Authored by: James Sousa (Mathispower4u.com) . License: Public Domain: No Known Copyright.
- System of 3 Equations with 3 Unknowns Application - Concentration Problem. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- System of 3 Equations with 3 Unknowns Application - Ticket Sales. Authored by: JAMES SOUSA (MATHISPOWER4U.COM) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
