We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

학습 가이드 > College Algebra

Sequences and Their Notations

A video game company launches an exciting new advertising campaign. They predict the number of online visits to their website, or hits, will double each day. The model they are using shows 2 hits the first day, 4 hits the second day, 8 hits the third day, and so on.
Day 1 2 3 4 5 …
Hits 2 4 8 16 32 …
If their model continues, how many hits will there be at the end of the month? To answer this question, we’ll first need to know how to determine a list of numbers written in a specific order. In this section, we will explore these kinds of ordered lists.

Sequences Defined by an Explicit Formula

One way to describe an ordered list of numbers is as a sequence. A sequence is a function whose domain is a subset of the counting numbers. The sequence established by the number of hits on the website is

[latex]\left\{2,4,8,16,32,\dots \right\}[/latex].

The ellipsis (…) indicates that the sequence continues indefinitely. Each number in the sequence is called a term. The first five terms of this sequence are 2, 4, 8, 16, and 32. Listing all of the terms for a sequence can be cumbersome. For example, finding the number of hits on the website at the end of the month would require listing out as many as 31 terms. A more efficient way to determine a specific term is by writing a formula to define the sequence. One type of formula is an explicit formula, which defines the terms of a sequence using their position in the sequence. Explicit formulas are helpful if we want to find a specific term of a sequence without finding all of the previous terms. We can use the formula to find the [latex]n\text{th}[/latex] term of the sequence, where [latex]n[/latex] is any positive number. In our example, each number in the sequence is double the previous number, so we can use powers of 2 to write a formula for the [latex]n\text{th}[/latex] term. Sequence of {2, 4, 8, 16, 32, ...} expressed in exponential form (i.e., {2^1, 2^2, 2^3, ..., 2^n, ...} The first term of the sequence is [latex]{2}^{1}=2[/latex], the second term is [latex]{2}^{2}=4[/latex], the third term is [latex]{2}^{3}=8[/latex], and so on. The [latex]n\text{th}[/latex] term of the sequence can be found by raising 2 to the [latex]n\text{th}[/latex] power. An explicit formula for a sequence is named by a lower case letter [latex]a,b,c..[/latex]. with the subscript [latex]n[/latex]. The explicit formula for this sequence is [latex]{a}_{n}={2}^{n}[/latex]. Now that we have a formula for the [latex]n\text{th}[/latex] term of the sequence, we can answer the question posed at the beginning of this section. We were asked to find the number of hits at the end of the month, which we will take to be 31 days. To find the number of hits on the last day of the month, we need to find the 31st term of the sequence. We will substitute 31 for [latex]n[/latex] in the formula.

[latex]\begin{array}{l}{a}_{31}={2}^{31}\hfill \\ \text{ }=\text{2,147,483,648}\hfill \end{array}[/latex]

If the doubling trend continues, the company will get [latex]\text{2,147,483,648}[/latex] hits on the last day of the month. That is over 2.1 billion hits! The huge number is probably a little unrealistic because it does not take consumer interest and competition into account. It does, however, give the company a starting point from which to consider business decisions. Another way to represent the sequence is by using a table. The first five terms of the sequence and the [latex]n\text{th}[/latex] term of the sequence are shown in the table.
[latex]n[/latex] 1 2 3 4 5 [latex]n[/latex]
[latex]n\text{th}[/latex] term of the sequence, [latex]{a}_{n}[/latex] 2 4 8 16 32 [latex]{2}^{n}[/latex]
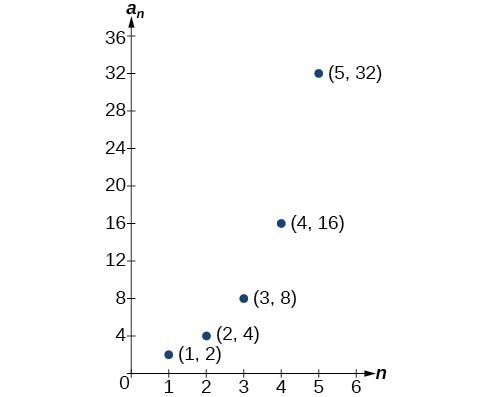Graphing provides a visual representation of the sequence as a set of distinct points. We can see from the graph below that the number of hits is rising at an exponential rate. This particular sequence forms an exponential function. Graph of a plotted exponential function, f(n) = 2^n, where the x-axis is labeled n and the y-axis is labeled a_n. Lastly, we can write this particular sequence as

[latex]\left\{2,4,8,16,32,\dots ,{2}^{n},\dots \right\}[/latex].

A sequence that continues indefinitely is called an infinite sequence. The domain of an infinite sequence is the set of counting numbers. If we consider only the first 10 terms of the sequence, we could write

[latex]\left\{2,4,8,16,32,\dots ,{2}^{n},\dots ,1024\right\}[/latex].

This sequence is called a finite sequence because it does not continue indefinitely.

A General Note: Sequence

A sequence is a function whose domain is the set of positive integers. A finite sequence is a sequence whose domain consists of only the first [latex]n[/latex] positive integers. The numbers in a sequence are called terms. The variable [latex]a[/latex] with a number subscript is used to represent the terms in a sequence and to indicate the position of the term in the sequence.

[latex]{a}_{1},{a}_{2},{a}_{3},\dots ,{a}_{n},\dots [/latex]

We call [latex]{a}_{1}[/latex] the first term of the sequence, [latex]{a}_{2}[/latex] the second term of the sequence, [latex]{a}_{3}[/latex] the third term of the sequence, and so on. The term [latex]{a}_{n}[/latex] is called the [latex]n\text{th}[/latex] term of the sequence, or the general term of the sequence. An explicit formula defines the [latex]n\text{th}[/latex] term of a sequence using the position of the term. A sequence that continues indefinitely is an infinite sequence.

Q & A

Does a sequence always have to begin with [latex]{a}_{1}?[/latex]

No. In certain problems, it may be useful to define the initial term as [latex]{a}_{0}[/latex] instead of [latex]{a}_{1}[/latex]. In these problems, the domain of the function includes 0.

How To: Given an explicit formula, write the first [latex]n[/latex] terms of a sequence.

  1. Substitute each value of [latex]n[/latex] into the formula. Begin with [latex]n=1[/latex] to find the first term, [latex]{a}_{1}[/latex].
  2. To find the second term, [latex]{a}_{2}[/latex], use [latex]n=2[/latex].
  3. Continue in the same manner until you have identified all [latex]n[/latex] terms.

Example: Writing the Terms of a Sequence Defined by an Explicit Formula

Write the first five terms of the sequence defined by the explicit formula [latex]{a}_{n}=-3n+8[/latex].

Answer: Substitute [latex]n=1[/latex] into the formula. Repeat with values 2 through 5 for [latex]n[/latex].

[latex]\begin{array}{llllll}n=1\hfill & \hfill & \hfill & \hfill & \hfill & {a}_{1}=-3\left(1\right)+8=5\hfill \\ n=2\hfill & \hfill & \hfill & \hfill & \hfill & {a}_{2}=-3\left(2\right)+8=2\hfill \\ n=3\hfill & \hfill & \hfill & \hfill & \hfill & {a}_{3}=-3\left(3\right)+8=-1\hfill \\ n=4\hfill & \hfill & \hfill & \hfill & \hfill & {a}_{4}=-3\left(4\right)+8=-4\hfill \\ n=5\hfill & \hfill & \hfill & \hfill & \hfill & {a}_{5}=-3\left(5\right)+8=-7\hfill \end{array}[/latex] The first five terms are [latex]\left\{5,2,-1,-4,-7\right\}[/latex].

Analysis of the Solution

The sequence values can be listed in a table. A table is a convenient way to input the function into a graphing utility.
[latex]n[/latex] 1 2 3 4 5
[latex]{a}_{n}[/latex] 5 2 –1 –4 –7
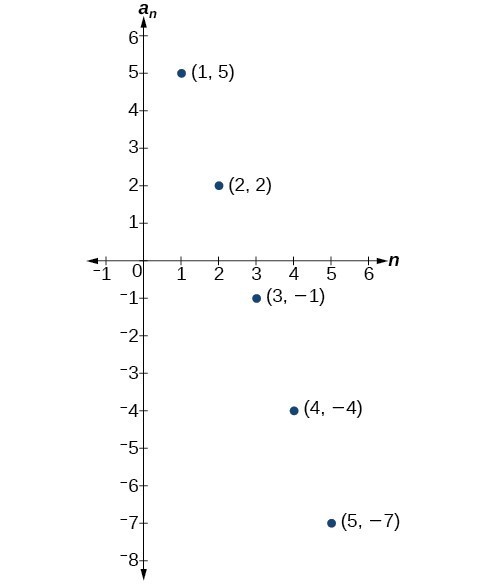
A graph can be made from this table of values. From the graph in Figure 2, we can see that this sequence represents a linear function, but notice the graph is not continuous because the domain is over the positive integers only. Graph of a scattered plot where the x-axis is labeled n and the y-axis is labeled a_n.

Try It

Write the first five terms of the sequence defined by the explicit formula [latex]{t}_{n}=5n - 4[/latex].

Answer: The first five terms are [latex]\left\{1,6, 11, 16, 21\right\}[/latex]

Try It

Write an explicit formula for the [latex]n\text{th}[/latex] term of the sequence.
[latex]\left\{-\frac{3}{4},-\frac{9}{8},-\frac{27}{12},-\frac{81}{16},-\frac{243}{20},...\right\}[/latex]

Answer: [latex]{a}_{n}=-\frac{{3}^{n}}{4n}[/latex]

Sequences Defined by a Recursive Formula

Sequences occur naturally in the growth patterns of nautilus shells, pinecones, tree branches, and many other natural structures. We may see the sequence in the leaf or branch arrangement, the number of petals of a flower, or the pattern of the chambers in a nautilus shell. Their growth follows the Fibonacci sequence, a famous sequence in which each term can be found by adding the preceding two terms. The numbers in the sequence are 1, 1, 2, 3, 5, 8, 13, 21, 34,…. Other examples from the natural world that exhibit the Fibonacci sequence are the Calla Lily, which has just one petal, the Black-Eyed Susan with 13 petals, and different varieties of daisies that may have 21 or 34 petals. Each term of the Fibonacci sequence depends on the terms that come before it. The Fibonacci sequence cannot easily be written using an explicit formula. Instead, we describe the sequence using a recursive formula, a formula that defines the terms of a sequence using previous terms. A recursive formula always has two parts: the value of an initial term (or terms), and an equation defining [latex]{a}_{n}[/latex] in terms of preceding terms. For example, suppose we know the following:

[latex]\begin{array}{l}{a}_{1}=3\hfill \\ {a}_{n}=2{a}_{n - 1}-1, \text{for} n\ge 2\hfill \end{array}[/latex]

We can find the subsequent terms of the sequence using the first term.

[latex]\begin{array}{l}{a}_{1}=3\\ {a}_{2}=2{a}_{1}-1=2\left(3\right)-1=5\\ {a}_{3}=2{a}_{2}-1=2\left(5\right)-1=9\\ {a}_{4}=2{a}_{3}-1=2\left(9\right)-1=17\end{array}[/latex]

So the first four terms of the sequence are [latex]\left\{3,\text{ }5,\text{ }9,\text{ }17\right\}[/latex] . The recursive formula for the Fibonacci sequence states the first two terms and defines each successive term as the sum of the preceding two terms.

[latex]\begin{array}{l}{a}_{1}=1\hfill \\ {a}_{2}=1\hfill \\ {a}_{n}={a}_{n - 1}+{a}_{n - 2}, \text{for} n\ge 3\hfill \end{array}[/latex]

To find the tenth term of the sequence, for example, we would need to add the eighth and ninth terms. We were told previously that the eighth and ninth terms are 21 and 34, so

[latex]{a}_{10}={a}_{9}+{a}_{8}=34+21=55[/latex]

A General Note: Recursive Formula

A recursive formula is a formula that defines each term of a sequence using preceding term(s). Recursive formulas must always state the initial term, or terms, of the sequence.

Q & A

Must the first two terms always be given in a recursive formula?

No. The Fibonacci sequence defines each term using the two preceding terms, but many recursive formulas define each term using only one preceding term. These sequences need only the first term to be defined.

How To: Given a recursive formula with only the first term provided, write the first [latex]n[/latex] terms of a sequence.

  1. Identify the initial term, [latex]{a}_{1}[/latex], which is given as part of the formula. This is the first term.
  2. To find the second term, [latex]{a}_{2}[/latex], substitute the initial term into the formula for [latex]{a}_{n - 1}[/latex]. Solve.
  3. To find the third term, [latex]{a}_{3}[/latex], substitute the second term into the formula. Solve.
  4. Repeat until you have solved for the [latex]n\text{th}[/latex] term.

Example: Writing the Terms of a Sequence Defined by a Recursive Formula

Write the first five terms of the sequence defined by the recursive formula.

[latex]\begin{array}{l}\begin{array}{l}\\ {a}_{1}=9\end{array}\hfill \\ {a}_{n}=3{a}_{n - 1}-20\text{, for }n\ge 2\hfill \end{array}[/latex]

Answer: The first term is given in the formula. For each subsequent term, we replace [latex]{a}_{n - 1}[/latex] with the value of the preceding term.

[latex]\begin{array}{ll}n=1\begin{array}{lllll}\hfill & \hfill & \hfill & \hfill & \hfill \end{array}\hfill & {a}_{1}=9\hfill \\ n=2\hfill & {a}_{2}=3{a}_{1}-20=3\left(9\right)-20=27 - 20=7\hfill \\ n=3\hfill & {a}_{3}=3{a}_{2}-20=3\left(7\right)-20=21 - 20=1\hfill \\ n=4\hfill & {a}_{4}=3{a}_{3}-20=3\left(1\right)-20=3 - 20=-17\hfill \\ n=5\hfill & {a}_{5}=3{a}_{4}-20=3\left(-17\right)-20=-51 - 20=-71\hfill \end{array}[/latex]

The first five terms are [latex]\left\{9,\text{ }7,\text{ }1,\text{ }-17,\text{ }-71\right\}[/latex]

Try It

Write the first five terms of the sequence defined by the recursive formula.

[latex]\begin{array}{l}{a}_{1}=2\\ {a}_{n}=2{a}_{n - 1}+1\text{, for }n\ge 2\end{array}[/latex]

Answer: [latex]\left\{2, 5, 11, 23, 47\right\}[/latex]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 5846, 5823. Authored by: Webwork-Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 5805, 5806, 5812. Authored by: David Lippman. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 6107. Authored by: Gregg Harbaugh. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 19458. Authored by: James Sousa. License: CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
  • Question ID 68773. Authored by: Roy Shahbazian. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Specific attribution