Series and Their Notations
A couple decides to start a college fund for their daughter. They plan to invest $50 in the fund each month. The fund pays 6% annual interest, compounded monthly. How much money will they have saved when their daughter is ready to start college in 6 years? In this section, we will learn how to answer this question. To do so, we need to consider the amount of money invested and the amount of interest earned.Arithmetic Series
Using Summation Notation
To find the total amount of money in the college fund and the sum of the amounts deposited, we need to add the amounts deposited each month and the amounts earned monthly. The sum of the terms of a sequence is called a series. Consider, for example, the following series.[latex]3+7+11+15+19+\cdots[/latex]
The [latex]n\text{th }[/latex] partial sum of a series is the sum of a finite number of consecutive terms beginning with the first term. The notation[latex]\text{ }{S}_{n}\text{ }[/latex] represents the partial sum. [latex]\begin{array}{l}{S}_{1}=3\\ {S}_{2}=3+7=10\\ {S}_{3}=3+7+11=21\\ {S}_{4}=3+7+11+15=36\end{array}[/latex]
Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma, [latex]\sigma[/latex], to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation, which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation, is the number used to generate the last term in a series.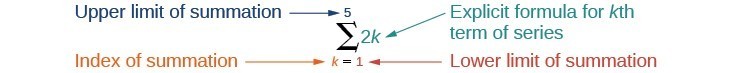 If we interpret the given notation, we see that it asks us to find the sum of the terms in the series [latex]{a}_{k}=2k[/latex] for [latex]k=1[/latex] through [latex]k=5[/latex]. We can begin by substituting the terms for [latex]k[/latex] and listing out the terms of this series.
If we interpret the given notation, we see that it asks us to find the sum of the terms in the series [latex]{a}_{k}=2k[/latex] for [latex]k=1[/latex] through [latex]k=5[/latex]. We can begin by substituting the terms for [latex]k[/latex] and listing out the terms of this series.
[latex]\begin{array}{l}\begin{array}{l}\\ {a}_{1}=2\left(1\right)=2\end{array}\hfill \\ {a}_{2}=2\left(2\right)=4\hfill \\ {a}_{3}=2\left(3\right)=6\hfill \\ {a}_{4}=2\left(4\right)=8\hfill \\ {a}_{5}=2\left(5\right)=10\hfill \end{array}[/latex]
We can find the sum of the series by adding the terms:[latex]\sum _{k=1}^{5}2k=2+4+6+8+10=30[/latex]
A General Note: Summation Notation
The sum of the first [latex]n[/latex] terms of a series can be expressed in summation notation as follows:[latex]\sum _{k=1}^{n}{a}_{k}[/latex]
This notation tells us to find the sum of [latex]{a}_{k}[/latex] from[latex]k=1[/latex] to [latex]k=n[/latex].
[latex]k[/latex] is called the index of summation, 1 is the lower limit of summation, and [latex]n[/latex] is the upper limit of summation.Q & A
Does the lower limit of summation have to be 1?
No. The lower limit of summation can be any number, but 1 is frequently used. We will look at examples with lower limits of summation other than 1.How To: Given summation notation for a series, evaluate the value.
- Identify the lower limit of summation.
- Identify the upper limit of summation.
- Substitute each value of [latex]k[/latex] from the lower limit to the upper limit into the formula.
- Add to find the sum.
Example: Using Summation Notation
Evaluate [latex]\sum _{k=3}^{7}{k}^{2}[/latex].Answer: According to the notation, the lower limit of summation is 3 and the upper limit is 7. So we need to find the sum of [latex]{k}^{2}[/latex] from [latex]k=3[/latex] to [latex]k=7[/latex]. We find the terms of the series by substituting [latex]k=3\text{,}4\text{,}5\text{,}6[/latex], and [latex]7[/latex] into the function [latex]{k}^{2}[/latex]. We add the terms to find the sum.
[latex]\begin{array}{ll}\sum _{k=3}^{7}{k}^{2}\hfill & ={3}^{2}+{4}^{2}+{5}^{2}+{6}^{2}+{7}^{2}\hfill \\ \hfill & =9+16+25+36+49\hfill \\ \hfill & =135\hfill \end{array}[/latex]
Try It
Evaluate [latex]\sum _{k=2}^{5}\left(3k - 1\right)[/latex].Answer: 38
Geometric Series
Just as the sum of the terms of an arithmetic sequence is called an arithmetic series, the sum of the terms in a geometric sequence is called a geometric series. Recall that a geometric sequence is a sequence in which the ratio of any two consecutive terms is the common ratio, [latex]r[/latex]. We can write the sum of the first [latex]n[/latex] terms of a geometric series as[latex]{S}_{n}={a}_{1}+r{a}_{1}+{r}^{2}{a}_{1}+...+{r}^{n - 1}{a}_{1}[/latex].
Just as with arithmetic series, we can do some algebraic manipulation to derive a formula for the sum of the first [latex]n[/latex] terms of a geometric series. We will begin by multiplying both sides of the equation by [latex]r[/latex].[latex]r{S}_{n}=r{a}_{1}+{r}^{2}{a}_{1}+{r}^{3}{a}_{1}+...+{r}^{n}{a}_{1}[/latex]
Next, we subtract this equation from the original equation.[latex]\begin{array}{l}\\ \frac{\begin{array}{l}\text{ }{S}_{n}={a}_{1}+r{a}_{1}+{r}^{2}{a}_{1}+...+{r}^{n - 1}{a}_{1}\hfill \\ -r{S}_{n}=-\left(r{a}_{1}+{r}^{2}{a}_{1}+{r}^{3}{a}_{1}+...+{r}^{n}{a}_{1}\right)\hfill \end{array}}{\left(1-r\right){S}_{n}={a}_{1}-{r}^{n}{a}_{1}}\end{array}[/latex]
Notice that when we subtract, all but the first term of the top equation and the last term of the bottom equation cancel out. To obtain a formula for [latex]{S}_{n}[/latex], divide both sides by[latex]\left(1-r\right)[/latex]. [latex]{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}\text{ r}\ne \text{1}[/latex]
A General Note: Formula for the Sum of the First n Terms of a Geometric Series
A geometric series is the sum of the terms in a geometric sequence. The formula for the sum of the first [latex]n[/latex] terms of a geometric sequence is represented as[latex]{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}\text{ r}\ne \text{1}[/latex]
How To: Given a geometric series, find the sum of the first n terms.
- Identify [latex]{a}_{1},r,\text{and}n[/latex].
- Substitute values for [latex]{a}_{1},r[/latex], and [latex]n[/latex] into the formula [latex]{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}[/latex].
- Simplify to find [latex]{S}_{n}[/latex].
Example: Finding the First n Terms of a Geometric Series
Use the formula to find the indicated partial sum of each geometric series.- [latex]{S}_{11}[/latex] for the series [latex]\text{ 8 + -4 + 2 + }\dots [/latex]
- [latex]\underset{6}{\overset{k=1}{{\sum }^{\text{ }}}}3\cdot {2}^{k}[/latex]
Answer:
- [latex]{a}_{1}=8[/latex], and we are given that [latex]n=11[/latex].We can find [latex]r[/latex] by dividing the second term of the series by the first. [latex-display]r=\frac{-4}{8}=-\frac{1}{2}[/latex-display] Substitute values for [latex]{a}_{1}, r, \text{and} n[/latex] into the formula and simplify. [latex]\begin{array}{l}{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}\hfill \\ {S}_{11}=\frac{8\left(1-{\left(-\frac{1}{2}\right)}^{11}\right)}{1-\left(-\frac{1}{2}\right)}\approx 5.336\hfill \end{array}[/latex]
- Find [latex]{a}_{1}[/latex] by substituting [latex]k=1[/latex] into the given explicit formula. [latex-display]{a}_{1}=3\cdot {2}^{1}=6[/latex-display] We can see from the given explicit formula that [latex]r=2[/latex]. The upper limit of summation is 6, so [latex]n=6[/latex].Substitute values for [latex]{a}_{1},r[/latex], and [latex]n[/latex] into the formula, and simplify. [latex]\begin{array}{l}{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}\hfill \\ {S}_{6}=\frac{6\left(1-{2}^{6}\right)}{1 - 2}=378\hfill \end{array}[/latex]
Try It
Use the formula to find the indicated partial sum of each geometric series. [latex-display]{S}_{20}[/latex] for the series [latex]\text{ 1,000 + 500 + 250 + }\dots [/latex-display]Answer: [latex]\approx 2,000.00[/latex]
Annuities
At the beginning of the section, we looked at a problem in which a couple invested a set amount of money each month into a college fund for six years. An annuity is an investment in which the purchaser makes a sequence of periodic, equal payments. To find the amount of an annuity, we need to find the sum of all the payments and the interest earned. In the example, the couple invests $50 each month. This is the value of the initial deposit. The account paid 6% annual interest, compounded monthly. To find the interest rate per payment period, we need to divide the 6% annual percentage interest (APR) rate by 12. So the monthly interest rate is 0.5%. We can multiply the amount in the account each month by 100.5% to find the value of the account after interest has been added. We can find the value of the annuity right after the last deposit by using a geometric series with [latex]{a}_{1}=50[/latex] and [latex]r=100.5%=1.005[/latex]. After the first deposit, the value of the annuity will be $50. Let us see if we can determine the amount in the college fund and the interest earned. We can find the value of the annuity after [latex]n[/latex] deposits using the formula for the sum of the first [latex]n[/latex] terms of a geometric series. In 6 years, there are 72 months, so [latex]n=72[/latex]. We can substitute [latex]{a}_{1}=50, r=1.005, \text{and} n=72[/latex] into the formula, and simplify to find the value of the annuity after 6 years.[latex]{S}_{72}=\frac{50\left(1-{1.005}^{72}\right)}{1 - 1.005}\approx 4\text{,}320.44[/latex]
After the last deposit, the couple will have a total of $4,320.44 in the account. Notice, the couple made 72 payments of $50 each for a total of [latex]72\left(50\right) = $3,600[/latex]. This means that because of the annuity, the couple earned $720.44 interest in their college fund.How To: Given an initial deposit and an interest rate, find the value of an annuity.
- Determine [latex]{a}_{1}[/latex], the value of the initial deposit.
- Determine [latex]n[/latex], the number of deposits.
- Determine [latex]r[/latex].
- Divide the annual interest rate by the number of times per year that interest is compounded.
- Add 1 to this amount to find [latex]r[/latex].
- Substitute values for [latex]{a}_{1}\text{,}r,\text{and}n[/latex] into the formula for the sum of the first [latex]n[/latex] terms of a geometric series, [latex]{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}[/latex].
- Simplify to find [latex]{S}_{n}[/latex], the value of the annuity after [latex]n[/latex] deposits.
Example: Solving an Annuity Problem
A deposit of $100 is placed into a college fund at the beginning of every month for 10 years. The fund earns 9% annual interest, compounded monthly, and paid at the end of the month. How much is in the account right after the last deposit?Answer: The value of the initial deposit is $100, so [latex]{a}_{1}=100[/latex]. A total of 120 monthly deposits are made in the 10 years, so [latex]n=120[/latex]. To find [latex]r[/latex], divide the annual interest rate by 12 to find the monthly interest rate and add 1 to represent the new monthly deposit.
[latex]r=1+\frac{0.09}{12}=1.0075[/latex]
Substitute [latex]{a}_{1}=100\text{,}r=1.0075\text{,}\text{and}n=120[/latex] into the formula for the sum of the first [latex]n[/latex] terms of a geometric series, and simplify to find the value of the annuity.[latex]{S}_{120}=\frac{100\left(1-{1.0075}^{120}\right)}{1 - 1.0075}\approx 19\text{,}351.43[/latex]
So the account has $19,351.43 after the last deposit is made.Try It
At the beginning of each month, $200 is deposited into a retirement fund. The fund earns 6% annual interest, compounded monthly, and paid into the account at the end of the month. How much is in the account if deposits are made for 10 years?Answer: $92,408.18
Key Equations
| sum of the first [latex]n[/latex] terms of an arithmetic series | [latex]{S}_{n}=\frac{n\left({a}_{1}+{a}_{n}\right)}{2}[/latex] |
| sum of the first [latex]n[/latex] terms of a geometric series | [latex]{S}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}\cdot r\ne 1[/latex] |
| sum of an infinite geometric series with [latex]-1<r<\text{ }1[/latex] | [latex]{S}_{n}=\frac{{a}_{1}}{1-r}\cdot r\ne 1[/latex] |
Key Concepts
- The sum of the terms in a sequence is called a series.
- A common notation for series is called summation notation, which uses the Greek letter sigma to represent the sum.
- The sum of the terms in an arithmetic sequence is called an arithmetic series.
- The sum of the first [latex]n[/latex] terms of an arithmetic series can be found using a formula.
- The sum of the terms in a geometric sequence is called a geometric series.
- The sum of the first [latex]n[/latex] terms of a geometric series can be found using a formula.
- The sum of an infinite series exists if the series is geometric with [latex]-1<r<1[/latex].
- If the sum of an infinite series exists, it can be found using a formula.
- An annuity is an account into which the investor makes a series of regularly scheduled payments. The value of an annuity can be found using geometric series.
Glossary
annuity an investment in which the purchaser makes a sequence of periodic, equal payments arithmetic series the sum of the terms in an arithmetic sequence diverge a series is said to diverge if the sum is not a real number geometric series the sum of the terms in a geometric sequence index of summation in summation notation, the variable used in the explicit formula for the terms of a series and written below the sigma with the lower limit of summation infinite series the sum of the terms in an infinite sequence lower limit of summation the number used in the explicit formula to find the first term in a series nth partial sum the sum of the first [latex]n[/latex] terms of a sequence series the sum of the terms in a sequence summation notation a notation for series using the Greek letter sigma; it includes an explicit formula and specifies the first and last terms in the series upper limit of summation the number used in the explicit formula to find the last term in a seriesLicenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 5865, 5867. Authored by: WebWork-Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY +GPL.
- Question ID 128790,128791. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 20277. Authored by: Kissel, Kris. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 23741. Authored by: Shahbazian, Roy, mb McClure, Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
