Real Numbers Review
Learning Objectives
- Real numbers
- Add and subtract real numbers
- Add real numbers with the same and different signs
- Subtract real numbers with the same and different signs
- Simplify combinations that require both addition and subtraction of real numbers.
- Multiply and divide real numbers
- Multiply two or more real numbers.
- Divide real numbers
- Simplify expressions with both multiplication and division
- Properties of real numbers
Real Numbers
Given any number n, we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers. As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative. The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line.Example: Classifying Real Numbers
Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?- [latex]-\frac{10}{3}[/latex]
- [latex]-6\pi[/latex]
- [latex]0.616161\dots[/latex]
- [latex] 0.13 [/latex]
Answer:
- [latex]-\frac{10}{3}[/latex] is negative and rational. It lies to the left of 0 on the number line.
- [latex]-6\pi [/latex] is negative and irrational. It lies to the left of 0.
- [latex]0.616161\dots [/latex] is a repeating decimal so it is rational and positive. It lies to the right of 0.
- [latex] 0.13 [/latex] is a finite decimal and may be written as 13/100. So it is rational and positive.
Try It
Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?- [latex]2\pi[/latex]
- [latex]-11.411411411\dots [/latex]
- [latex]\frac{47}{19}[/latex]
- [latex]6.210735[/latex]
Answer:
- positive, irrational; right
- negative, rational; left
- positive, rational; right
- positive, rational; right
Sets of Numbers as Subsets
Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram.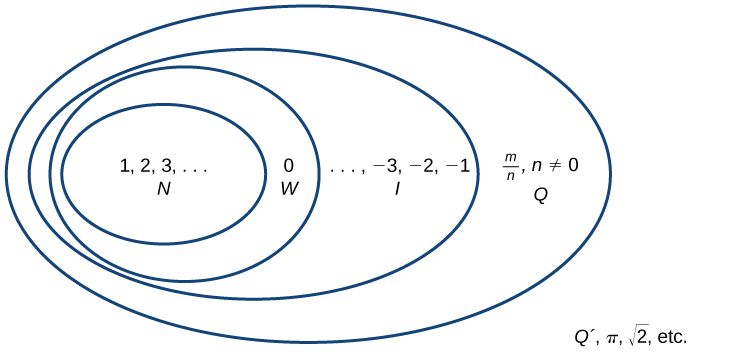 Sets of numbers. N: the set of natural numbers W: the set of whole numbers I: the set of integers Q: the set of rational numbers Q´: the set of irrational numbers
Sets of numbers. N: the set of natural numbers W: the set of whole numbers I: the set of integers Q: the set of rational numbers Q´: the set of irrational numbersA General Note: Sets of Numbers
The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex]. The set of whole numbers is the set of natural numbers plus zero: [latex]\{0,1,2,3,\dots\}[/latex]. The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex]. The set of rational numbers includes fractions written as [latex]\{\frac{m}{n}|m\text{ and }n\text{ are integers and }n\ne 0\}[/latex]. The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: [latex]\{h|h\text{ is not a rational number}\}[/latex].Adding and Subtracting Real Numbers
When adding integers we have two cases to consider. The first case is whether the signs match (both positive or both negative). If the signs match, we will add the numbers together and keep the sign. If the signs don’t match (one positive and one negative number) we will subtract the numbers (as if they were all positive) and then use the sign from the larger number. This means if the larger number is positive, the answer is positive. If the larger number is negative, the answer is negative.To add two numbers with the same sign (both positive or both negative)
- Add their absolute values (without the [latex]+[/latex] or [latex]-[/latex] sign)
- Give the sum the same sign.
To add two numbers with different signs (one positive and one negative)
- Find the difference of their absolute values. (Note that when you find the difference of the absolute values, you always subtract the lesser absolute value from the greater one.)
- Give the sum the same sign as the number with the greater absolute value.
Example
Find [latex]23–73[/latex].Answer: You can't use your usual method of subtraction because 73 is greater than 23. Rewrite the subtraction as adding the opposite.
[latex]23+\left(−73\right)[/latex]
The addends have different signs, so find the difference of their absolute values.[latex]\begin{array}{c}\left|23\right|=23\,\,\,\text{and}\,\,\,\left|−73\right|=73\\73-23=50\end{array}[/latex]
Since [latex]\left|−73\right|>\left|23\right|[/latex], the final answer is negative.Answer
[latex-display]23–73=−50[/latex-display]
Example
Find [latex]382–\left(−93\right)[/latex].Answer: You are subtracting a negative, so think of this as taking the negative sign away. This becomes an addition problem. [latex]-93[/latex] becomes [latex]+93[/latex]
[latex]382+93=475[/latex]
Answer
[latex-display]382–(−93)=475[/latex-display]Example
Find [latex]-\frac{3}{7}-\frac{6}{7}+\frac{2}{7}[/latex]Answer: Add the first two and give the result a negative sign: Since the signs of the first two are the same, find the sum of the absolute values of the fractions Since both numbers are negative, the sum is negative. If you owe money, then borrow more, the amount you owe becomes larger.
[latex]\left| -\frac{3}{7} \right|=\frac{3}{7}[/latex] and [latex]\left| -\frac{6}{7} \right|=\frac{6}{7}[/latex]
[latex]\begin{array}{c}\frac{3}{7}+\frac{6}{7}=\frac{9}{7}\\\\-\frac{3}{7}-\frac{6}{7} =-\frac{9}{7}\end{array}[/latex]
Now add the third number. The signs are different, so find the difference of their absolute values.[latex] \left| -\frac{9}{7} \right|=\frac{9}{7}[/latex] and [latex] \left| \frac{2}{7} \right|=\frac{2}{7}[/latex]
[latex] \frac{9}{7}-\frac{2}{7}=\frac{7}{7}[/latex]
Since [latex]\left|\frac{-9}{7}\right|>\left|\frac{2}{7}\right|[/latex], the sign of the final sum is the same as the sign of [latex]-\frac{9}{7}[/latex].[latex] -\frac{9}{7}+\frac{2}{7}=-\frac{7}{7}[/latex]
Answer
[latex-display]-\frac{3}{7}+\left(-\frac{6}{7}\right)+\frac{2}{7}=-\frac{7}{7}[/latex-display]Example
Evaluate [latex]27.832+(−3.06)[/latex]. When you add decimals, remember to line up the decimal points so you are adding tenths to tenths, hundredths to hundredths, and so on.Answer: Since the addends have different signs, subtract their absolute values.
[latex] \begin{array}{r}\underline{\begin{array}{r}27.832\\-\text{ }3.06\,\,\,\end{array}}\\24.772\end{array}[/latex]
[latex]\left|-3.06\right|=3.06[/latex]
The sum has the same sign as 27.832 whose absolute value is greater.Answer
[latex-display]27.832+\left(-3.06\right)=24.772[/latex-display]Multiplying and Dividing Real Numbers
Multiplication and division are inverse operations, just as addition and subtraction are. You may recall that when you divide fractions, you multiply by the reciprocal. Inverse operations "undo" each other.Multiply Real Numbers
Multiplying real numbers is not that different from multiplying whole numbers and positive fractions. However, you haven't learned what effect a negative sign has on the product. With whole numbers, you can think of multiplication as repeated addition. Using the number line, you can make multiple jumps of a given size. For example, the following picture shows the product [latex]3\cdot4[/latex] as 3 jumps of 4 units each.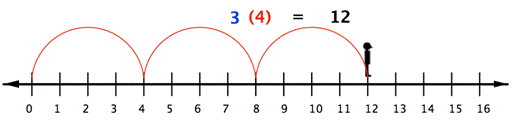 So to multiply [latex]3(−4)[/latex], you can face left (toward the negative side) and make three “jumps” forward (in a negative direction).
So to multiply [latex]3(−4)[/latex], you can face left (toward the negative side) and make three “jumps” forward (in a negative direction).
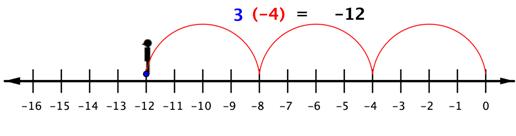 The product of a positive number and a negative number (or a negative and a positive) is negative.
The product of a positive number and a negative number (or a negative and a positive) is negative.
The Product of a Positive Number and a Negative Number
To multiply a positive number and a negative number, multiply their absolute values. The product is negative.Example
Find [latex]−3.8(0.6)[/latex].Answer: Multiply the absolute values as you normally would. Place the decimal point by counting place values. 3.8 has 1 place after the decimal point, and 0.6 has 1 place after the decimal point, so the product has [latex]1+1[/latex] or 2 places after the decimal point.
[latex]\begin{array}{r}3.8\\\underline{\times\,\,\,0.6}\\2.28\end{array}[/latex]
The product of a negative and a positive is negative.Answer
[latex-display]−3.8(0.6)=−2.28[/latex-display]The Product of Two Numbers with the Same Sign (both positive or both negative)
To multiply two positive numbers, multiply their absolute values. The product is positive. To multiply two negative numbers, multiply their absolute values. The product is positive.Example
Find [latex] ~\left( -\frac{3}{4} \right)\left( -\frac{2}{5} \right)[/latex]Answer: Multiply the absolute values of the numbers. First, multiply the numerators together to get the product's numerator. Then, multiply the denominators together to get the product's denominator. Rewrite in lowest terms, if needed.
[latex] \left( \frac{3}{4} \right)\left( \frac{2}{5} \right)=\frac{6}{20}=\frac{3}{10}[/latex]
The product of two negative numbers is positive.Answer
[latex-display] \left( -\frac{3}{4} \right)\left( -\frac{2}{5} \right)=\frac{3}{10}[/latex-display]- positive [latex]\cdot[/latex] positive: The product is positive.
- negative [latex]\cdot[/latex] negative: The product is positive.
- negative [latex]\cdot[/latex] positive: The product is negative.
- positive [latex]\cdot[/latex] negative: The product is negative.
Multiplying More Than Two Negative Numbers
If there are an even number (0, 2, 4, ...) of negative factors to multiply, the product is positive. If there are an odd number (1, 3, 5, ...) of negative factors, the product is negative.Example
Find [latex]3(−6)(2)(−3)(−1)[/latex].Answer: Multiply the absolute values of the numbers.
[latex]\begin{array}{l}3(6)(2)(3)(1)\\18(2)(3)(1)\\36(3)(1)\\108(1)\\108\end{array}[/latex]
Count the number of negative factors. There are three [latex]\left(−6,−3,−1\right)[/latex].[latex]3(−6)(2)(−3)(−1)[/latex]
Since there are an odd number of negative factors, the product is negative.Answer
[latex-display]3(−6)(2)(−3)(−1)=−108[/latex-display]Divide Real Numbers
You may remember that when you divided fractions, you multiplied by the reciprocal. Reciprocal is another name for the multiplicative inverse (just as opposite is another name for additive inverse). An easy way to find the multiplicative inverse is to just “flip” the numerator and denominator as you did to find the reciprocal. Here are some examples:- The reciprocal of [latex]\frac{4}{9}[/latex] is [latex] \frac{9}{4}[/latex]because [latex]\frac{4}{9}\left(\frac{9}{4}\right)=\frac{36}{36}=1[/latex].
- The reciprocal of 3 is [latex]\frac{1}{3}[/latex] because [latex]\frac{3}{1}\left(\frac{1}{3}\right)=\frac{3}{3}=1[/latex].
- The reciprocal of [latex]-\frac{5}{6}[/latex] is [latex]\frac{-6}{5}[/latex] because [latex]-\frac{5}{6}\left( -\frac{6}{5} \right)=\frac{30}{30}=1[/latex].
- The reciprocal of 1 is 1 as [latex]1(1)=1[/latex].
[latex] 26\div 2=26\left( \frac{1}{2} \right)=13[/latex]
Notice that 2 and [latex] \frac{1}{2}[/latex] are reciprocals. Try again, dividing a bag of 36 marbles into smaller bags.| Number of bags | Dividing by number of bags | Multiplying by reciprocal |
|---|---|---|
| 3 | [latex]\frac{36}{3}=12[/latex] | [latex] 36\left( \frac{1}{3} \right)=\frac{36}{3}=\frac{12(3)}{3}=12[/latex] |
| 4 | [latex]\frac{36}{4}=9[/latex] | [latex]36\left(\frac{1}{4}\right)=\frac{36}{4}=\frac{9\left(4\right)}{4}=9[/latex] |
| 6 | [latex]\frac{36}{6}=6[/latex] | [latex]36\left(\frac{1}{6}\right)=\frac{36}{6}=\frac{6\left(6\right)}{6}=6[/latex] |
Example
Find [latex] 28\div \frac{4}{3}[/latex]Answer: Rewrite the division as multiplication by the reciprocal. The reciprocal of [latex] \frac{4}{3}[/latex] is [latex]\frac{3}{4} [/latex].
[latex] 28\div \frac{4}{3}=28\left( \frac{3}{4} \right)[/latex]
Multiply.[latex]\frac{28}{1}\left(\frac{3}{4}\right)=\frac{28\left(3\right)}{4}=\frac{4\left(7\right)\left(3\right)}{4}=7\left(3\right)=21[/latex]
Answer
[latex-display]28\div\frac{4}{3}=21[/latex-display]Rules of Division
When dividing, rewrite the problem as multiplication using the reciprocal of the divisor as the second factor. When one number is positive and the other is negative, the quotient is negative. When both numbers are negative, the quotient is positive. When both numbers are positive, the quotient is positive.Example
Find [latex]24\div\left(-\frac{5}{6}\right)[/latex].Answer: Rewrite the division as multiplication by the reciprocal.
[latex] 24\div \left( -\frac{5}{6} \right)=24\left( -\frac{6}{5} \right)[/latex]
Multiply. Since one number is positive and one is negative, the product is negative.[latex] \frac{24}{1}\left( -\frac{6}{5} \right)=-\frac{144}{5}[/latex]
Answer
[latex-display] 24\div \left( -\frac{5}{6} \right)=-\frac{144}{5}[/latex-display]Example
Find [latex] 4\,\left( -\frac{2}{3} \right)\,\div \left( -6 \right)[/latex]Answer: Rewrite the division as multiplication by the reciprocal.
[latex] \frac{4}{1}\left( -\frac{2}{3} \right)\left( -\frac{1}{6} \right)[/latex]
Multiply. There is an even number of negative numbers, so the product is positive.[latex]\frac{4\left(2\right)\left(1\right)}{3\left(6\right)}=\frac{8}{18}[/latex]
Write the fraction in lowest terms.Answer
[latex-display] 4\left( -\frac{2}{3} \right)\div \left( -6 \right)=\frac{4}{9}[/latex-display] Remember that a fraction bar also indicates division, so a negative sign in front of a fraction goes with the numerator, the denominator, or the whole fraction: [latex]-\frac{3}{4}=\frac{-3}{4}=\frac{3}{-4}[/latex].
In each case, the overall fraction is negative because there's only one negative in the division.
Remember that a fraction bar also indicates division, so a negative sign in front of a fraction goes with the numerator, the denominator, or the whole fraction: [latex]-\frac{3}{4}=\frac{-3}{4}=\frac{3}{-4}[/latex].
In each case, the overall fraction is negative because there's only one negative in the division.
Properties of Real Numbers
Commutative Properties
The commutative property of addition states that numbers may be added in any order without affecting the sum.Associative Properties
The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.Distributive Property
The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.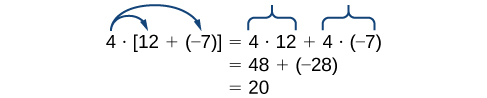 Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.Inverse Properties
The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted−a, that, when added to the original number, results in the additive identity, 0.A General Note: Properties of Real Numbers
The following properties hold for real numbers a, b, and c.| Addition | Multiplication | |
|---|---|---|
| Commutative Property | [latex]a+b=b+a[/latex] | [latex]a\cdot b=b\cdot a[/latex] |
| Associative Property | [latex]a+\left(b+c\right)=\left(a+b\right)+c[/latex] | [latex]a\left(bc\right)=\left(ab\right)c[/latex] |
| Distributive Property | [latex]a\cdot \left(b+c\right)=a\cdot b+a\cdot c[/latex] | |
| Identity Property | There exists a unique real number called the additive identity, 0, such that, for any real number a
[latex]a+0=a[/latex] |
There exists a unique real number called the multiplicative identity, 1, such that, for any real number a
[latex]a\cdot 1=a[/latex] |
| Inverse Property | Every real number a has an additive inverse, or opposite, denoted –a, such that
[latex]a+\left(-a\right)=0[/latex] |
Every nonzero real number a has a multiplicative inverse, or reciprocal, denoted [latex]\frac{1}{a}[/latex], such that
[latex]a\cdot \left(\frac{1}{a}\right)=1[/latex] |
Example: Using Properties of Real Numbers
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.- [latex]3\cdot 6+3\cdot 4[/latex]
- [latex]\left(5+8\right)+\left(-8\right)[/latex]
- [latex]6-\left(15+9\right)[/latex]
- [latex]\frac{4}{7}\cdot \left(\frac{2}{3}\cdot \frac{7}{4}\right)[/latex]
- [latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]
Answer:
- [latex]\begin{array}\text{ }3\cdot6+3\cdot4 \hfill& =3\cdot\left(6+4\right) \hfill& \text{Distributive property} \\ \hfill& =3\cdot10 \hfill& \text{Simplify} \\ \hfill& =30 \hfill& \text{Simplify}\end{array}[/latex]
- [latex]\begin{array}\text{ }\left(5+8\right)+\left(-8\right) \hfill& =5+\left[8+\left(-8\right)\right] \hfill& \text{Associative property of addition} \\ &\hfill =5+0 \hfill& \text{Inverse property of addition} \\ \hfill& =5 \hfill& \text{Identity property of addition}\end{array}[/latex]
- [latex]\begin{array}6-\left(15+9\right) \hfill& =6+[15\left(-15\right)+\left(-9\right)] \hfill& \text{Distributive property} \\ \hfill& =6+\left(-24\right) \hfill& \text{Simplify} \\ \hfill& =-18 \hfill& \text{Simplify}\end{array}[/latex]
- [latex]\begin{array}\text{ }\frac{4}{7}\cdot\left(\frac{2}{3}\cdot\frac{7}{4}\right) \hfill& =\frac{4}{7} \cdot\left(\frac{7}{4}\cdot\frac{2}{3}\right) \hfill& \text{Commutative property of multiplication} \\ \hfill& =\left(\frac{4}{7}\cdot\frac{7}{4}\right)\cdot\frac{2}{3}\hfill& \text{Associative property of multiplication} \\ \hfill& =1\cdot\frac{2}{3} \hfill& \text{Inverse property of multiplication} \\ \hfill& =\frac{2}{3} \hfill& \text{Identity property of multiplication}\end{array}[/latex]
- [latex]\begin{array}\text{ }100\cdot[0.75+\left(-2.38\right)] \hfill& =100\cdot0.75+100\cdot\left(-2.38\right)\hfill& \text{Distributive property} \\ \hfill& =75+\left(-238\right) \hfill& \text{Simplify} \\ \hfill& =-163 \hfill& \text{Simplify}\end{array}[/latex]
Try It
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.- [latex]\left(-\frac{23}{5}\right)\cdot \left[11\cdot \left(-\frac{5}{23}\right)\right][/latex]
- [latex]5\cdot \left(6.2+0.4\right)[/latex]
- [latex]18-\left(7 - 15\right)[/latex]
- [latex]6\cdot \left(-3\right)+6\cdot 3[/latex]
Answer:
- commutative property of multiplication, associative property of multiplication, inverse property of multiplication, identity property of multiplication;
- 33, distributive property;
- 26, distributive property;
- 0, distributive property, inverse property of addition, identity property of addition
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 2: Subtracting Integers (Two Digit Integers). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Find the Sum and Difference of Three Signed Fractions (Common Denom). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Unit 9: Real Numbers, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex: Multiplying Three or More Integers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: Multiplying Signed Fractions . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 1: Dividing Signed Fractions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Authored by: College Algebra. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Identifying Sets of Real Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
