Adding and Subtracting Radicals
Learning Outcomes
- Identify radicals that can be added or subtracted
- Add and subtract radical expressions
[latex]5x+3y - 4x+7y=x+10y[/latex]
There are two keys to combining radicals by addition or subtraction: look at the index, and look at the radicand. If these are the same, then addition and subtraction are possible. If not, then you cannot combine the two radicals. Remember the index is the degree of the root and the radicand is the term or expression under the radical. In the diagram below, the index is n, and the radicand is [latex]100[/latex]. The radicand is placed under the root symbol and the index is placed outside the root symbol to the left: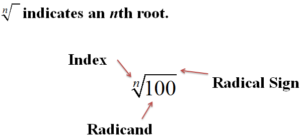 Index and radicand
Index and radicand Practice identifying radicals that are compatible for addition and subtraction by looking at the index and radicand of the roots in the following example.
Practice identifying radicals that are compatible for addition and subtraction by looking at the index and radicand of the roots in the following example.
Example
Identify the roots that have the same index and radicand. [latex-display] 10\sqrt{6}[/latex-display] [latex-display] -1\sqrt[3]{6}[/latex-display] [latex-display] \sqrt{25}[/latex-display] [latex-display] 12\sqrt{6}[/latex-display] [latex-display] \frac{1}{2}\sqrt[3]{25}[/latex-display] [latex-display] -7\sqrt[3]{6}[/latex-display]Answer: Let's start with [latex] 10\sqrt{6}[/latex]. The index is [latex]2[/latex] because no root was specified, and the radicand is [latex]6[/latex]. The only other radical that has the same index and radicand is [latex] 12\sqrt{6}[/latex]. [latex] -1\sqrt[3]{6}[/latex] has an index of [latex]3[/latex], and a radicand of [latex]6[/latex]. The only other radical that has the same index and radicand is [latex] -7\sqrt[3]{6}[/latex]. [latex] \sqrt{25}[/latex] has an index of [latex]2[/latex] and a radicand of [latex]25[/latex]. There are no other radicals in the list that have the same index and radicand. [latex-display] 12\sqrt{6}[/latex] has the same index and radicand as [latex]10\sqrt{6}[/latex-display] [latex] \frac{1}{2}\sqrt[3]{25}[/latex] has an index of [latex]3[/latex] and a radicand of [latex]25[/latex]. There are no other radicals in the list that share these. [latex-display] -7\sqrt[3]{6}[/latex] has the same index and radicand as [latex] -1\sqrt[3]{6}[/latex-display]
Example
Add. [latex] 3\sqrt{11}+7\sqrt{11}[/latex]Answer: The two radicals have the same index and radicand. This means you can combine them as you would combine the terms [latex] 3a+7a[/latex].
[latex] \text{3}\sqrt{11}\text{ + 7}\sqrt{11}[/latex]
Answer
[latex-display] 3\sqrt{11}+7\sqrt{11}=10\sqrt{11}[/latex-display]Example
Add. [latex] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}[/latex]Answer: Rearrange terms so that like radicals are next to each other. Then add.
[latex] 5\sqrt{2}+2\sqrt{2}+\sqrt{3}+4\sqrt{3}[/latex]
Answer
[latex-display] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}=7\sqrt{2}+5\sqrt{3}[/latex-display]Example
Add. [latex] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}[/latex]Answer: Rearrange terms so that like radicals are next to each other. Then add.
[latex] 3\sqrt{x}+\sqrt{x}+12\sqrt[3]{xy}[/latex]
Answer
[latex-display] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}=4\sqrt{x}+12\sqrt[3]{xy}[/latex-display]Try It
[ohm_question]3493[/ohm_question]Example
Add and simplify. [latex] 2\sqrt[3]{40}+\sqrt[3]{135}[/latex]Answer: Simplify each radical by identifying perfect cubes.
[latex] \begin{array}{r}2\sqrt[3]{8\cdot 5}+\sqrt[3]{27\cdot 5}\\2\sqrt[3]{{{(2)}^{3}}\cdot 5}+\sqrt[3]{{{(3)}^{3}}\cdot 5}\\2\sqrt[3]{{{(2)}^{3}}}\cdot \sqrt[3]{5}+\sqrt[3]{{{(3)}^{3}}}\cdot \sqrt[3]{5}\end{array}[/latex]
Simplify.[latex] 2\cdot 2\cdot \sqrt[3]{5}+3\cdot \sqrt[3]{5}[/latex]
Add.[latex]4\sqrt[3]{5}+3\sqrt[3]{5}[/latex]
Answer
[latex-display] 2\sqrt[3]{40}+\sqrt[3]{135}=7\sqrt[3]{5}[/latex-display]Example
Add and simplify. [latex] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}[/latex]Answer: Simplify each radical by identifying perfect cubes.
[latex]\begin{array}{r}x\sqrt[3]{x\cdot {{y}^{3}}\cdot y}+y\sqrt[3]{{{x}^{3}}\cdot x\cdot y}\\x\sqrt[3]{{{y}^{3}}}\cdot \sqrt[3]{xy}+y\sqrt[3]{{{x}^{3}}}\cdot \sqrt[3]{xy}\\xy\cdot \sqrt[3]{xy}+xy\cdot \sqrt[3]{xy}\end{array}[/latex]
Add like radicals.[latex] xy\sqrt[3]{xy}+xy\sqrt[3]{xy}[/latex]
Answer
[latex-display] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}=2xy\sqrt[3]{xy}[/latex-display]Subtracting Radicals
Subtraction of radicals follows the same set of rules and approaches as addition—the radicands and the indices (plural of index) must be the same for two (or more) radicals to be subtracted. In the examples that follow, subtraction has been rewritten as addition of the opposite.Example
Subtract. [latex] 5\sqrt{13}-3\sqrt{13}[/latex]Answer: The radicands and indices are the same, so these two radicals can be combined.
[latex] 5\sqrt{13}-3\sqrt{13}[/latex]
Answer
[latex-display] 5\sqrt{13}-3\sqrt{13}=2\sqrt{13}[/latex-display]Example
Subtract. [latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}[/latex]Answer: Two of the radicals have the same index and radicand, so they can be combined. Rewrite the expression so that like radicals are next to each other.
[latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}\\4\sqrt[3]{5a}-2\sqrt[3]{5a})-\sqrt[3]{3a})[/latex]
Combine. Although the indices of [latex] 2\sqrt[3]{5a}[/latex] and [latex] -\sqrt[3]{3a}[/latex] are the same, the radicands are not—so they cannot be combined.[latex] 2\sqrt[3]{5a}-\sqrt[3]{3a})[/latex]
Answer
[latex-display] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}=2\sqrt[3]{5a}-\sqrt[3]{3a}[/latex-display]Example
Subtract and simplify. [latex] 5\sqrt[4]{{{a}^{5}}b}-a\sqrt[4]{16ab}[/latex], where [latex]a\ge 0[/latex] and [latex]b\ge 0[/latex]Answer: Simplify each radical by identifying and pulling out powers of [latex]4[/latex].
[latex]\begin{array}{r}5\sqrt[4]{{{a}^{4}}\cdot a\cdot b}-a\sqrt[4]{{{(2)}^{4}}\cdot a\cdot b}\\5\cdot a\sqrt[4]{a\cdot b}-a\cdot 2\sqrt[4]{a\cdot b}\\5a\sqrt[4]{ab}-2a\sqrt[4]{ab}\end{array}[/latex]
The answer is [latex]3a\sqrt[4]{ab}[/latex].Summary
Combining radicals is possible when the index and the radicand of two or more radicals are the same. Radicals with the same index and radicand are known as like radicals. It is often helpful to treat radicals just as you would treat variables: like radicals can be added and subtracted in the same way that like variables can be added and subtracted. Sometimes, you will need to simplify a radical expression before it is possible to add or subtract like terms.Contribute!
Licenses & Attributions
CC licensed content, Original
- Screenshot: keys. Provided by: Lumen Learning License: CC BY: Attribution.
- Screenshot: Index and radicand. Provided by: Lumen Learning License: CC BY: Attribution.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex: Add and Subtract Radicals - No Simplifying. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: Add and Subtract Square Roots. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
