Notation and Modeling Subtraction of Integers
Learning Outcomes
- Model integer subtraction with color counters
- [latex]5 - 3[/latex]
- [latex]- 5-\left(-3\right)[/latex]
- [latex]-5 - 3[/latex]
- [latex]5-\left(-3\right)[/latex]
example
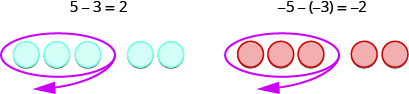
Model: [latex]5 - 3[/latex]. Solution:| Interpret the expression. | [latex]5 - 3[/latex] means [latex]5[/latex] take away [latex]3[/latex] . |
| Model the first number. Start with [latex]5[/latex] positives. |  |
| Take away the second number. So take away [latex]3[/latex] positives. |  |
| Find the counters that are left. |  |
| [latex]5 - 3=2[/latex] . The difference between [latex]5[/latex] and [latex]3[/latex] is [latex]2[/latex] . |
try it
Model the expression: [latex-display]6 - 4[/latex-display]Answer:
 [latex-display]2[/latex-display]
[latex-display]2[/latex-display]
Answer:
 [latex-display]3[/latex-display]
[latex-display]3[/latex-display]
example
Model: [latex]-5-\left(-3\right)[/latex]Answer: Solution:
| Interpret the expression. | [latex]-5-\left(-3\right)[/latex] means [latex]-5[/latex] take away [latex]-3[/latex] . |
| Model the first number. Start with [latex]5[/latex] negatives. |  |
| Take away the second number. So take away [latex]3[/latex] negatives. |  |
| Find the number of counters that are left. |  |
| [latex]-5-\left(-3\right)=-2[/latex] . The difference between [latex]-5[/latex] and [latex]-3[/latex] is [latex]-2[/latex] . |
try it
Model the expression: [latex-display]-6-\left(-4\right)[/latex-display]Answer:
 [latex-display]−2[/latex-display]
[latex-display]−2[/latex-display]
Answer:
 [latex-display]−3[/latex-display]
[latex-display]−3[/latex-display]
- First, we subtracted [latex]3[/latex] positives from [latex]5[/latex] positives to get [latex]2[/latex] positives.
- Then we subtracted [latex]3[/latex] negatives from [latex]5[/latex] negatives to get [latex]2[/latex] negatives.
 Now let’s see what happens when we subtract one positive and one negative number. We will need to use both positive and negative counters and sometimes some neutral pairs, too. Adding a neutral pair does not change the value.
Now let’s see what happens when we subtract one positive and one negative number. We will need to use both positive and negative counters and sometimes some neutral pairs, too. Adding a neutral pair does not change the value.
example
Model: [latex]-5 - 3[/latex].Answer: Solution:
| Interpret the expression. | [latex]-5 - 3[/latex] means [latex]-5[/latex] take away [latex]3[/latex] . |
| Model the first number. Start with [latex]5[/latex] negatives. |  |
| Take away the second number. So we need to take away [latex]3[/latex] positives. | |
| But there are no positives to take away. Add neutral pairs until you have [latex]3[/latex] positives. |  |
| Now take away [latex]3[/latex] positives. |  |
| Count the number of counters that are left. |  |
| [latex]-5 - 3=-8[/latex] . The difference of [latex]-5[/latex] and [latex]3[/latex] is [latex]-8[/latex] . |
try it
Model the expression: [latex-display]-6 - 4[/latex-display]Answer:
 [latex-display]−10[/latex-display]
[latex-display]−10[/latex-display]
Answer:
 [latex-display]−11[/latex-display]
[latex-display]−11[/latex-display]
example
Model: [latex]5-\left(-3\right)[/latex].Answer: Solution:
| Interpret the expression. | [latex]5-\left(-3\right)[/latex] means [latex]5[/latex] take away [latex]-3[/latex] . |
| Model the first number. Start with [latex]5[/latex] positives. |  |
| Take away the second number, so take away [latex]3[/latex] negatives. | |
| But there are no negatives to take away. Add neutral pairs until you have [latex]3[/latex] negatives. |  |
| Then take away [latex]3[/latex] negatives. |  |
| Count the number of counters that are left. |  |
| The difference of [latex]5[/latex] and [latex]-3[/latex] is [latex]8[/latex] . [latex]5-\left(-3\right)=8[/latex] |
try it
Model the expression: [latex-display]6-\left(-4\right)[/latex-display]Answer:
 [latex-display]10[/latex-display]
[latex-display]10[/latex-display]
Answer:
 [latex-display]11[/latex-display]
[latex-display]11[/latex-display]
- subtracting a positive number from a positive number
- subtracting a positive number from a negative number
- subtracting a negative number from a positive number
- subtracting a negative number from a negative number
example
Model each subtraction. [latex-display]8 − 2[/latex-display] [latex-display]−5 − 4[/latex-display] [latex-display]6 − (−6)[/latex-display] [latex-display]−8 − (−3)[/latex-display]Answer:
| 1. | |
| [latex]8 - 2[/latex] This means [latex]8[/latex] take away [latex]2[/latex] . | |
| Start with [latex]8[/latex] positives. |  |
| Take away [latex]2[/latex] positives. |  |
| How many are left? | [latex]6[/latex] |
| [latex]8 - 2=6[/latex] |
| 2. | |
| [latex]-5 - 4[/latex] This means [latex]-5[/latex] take away [latex]4[/latex] . | |
| Start with [latex]5[/latex] negatives. |  |
| You need to take away [latex]4[/latex] positives. Add [latex]4[/latex] neutral pairs to get [latex]4[/latex] positives. | 
 |
| Take away [latex]4[/latex] positives. |  |
| How many are left? |  |
| [latex]-9[/latex] | |
| [latex]-5 - 4=-9[/latex] |
| 3. | |
| [latex]6-\left(-6\right)[/latex] This means [latex]6[/latex] take away [latex]-6[/latex] . | |
| Start with [latex]6[/latex] positives. |  |
| Add [latex]6[/latex] neutrals to get [latex]6[/latex] negatives to take away. |  |
| Remove [latex]6[/latex] negatives. |  |
| How many are left? |  |
| [latex]12[/latex] | |
| [latex]6-\left(-6\right)=12[/latex] |
| 4. | |
| [latex]-8-\left(-3\right)[/latex] This means [latex]-8[/latex] take away [latex]-3[/latex] . | |
| Start with [latex]8[/latex] negatives. |  |
| Take away [latex]3[/latex] negatives. |  |
| How many are left? |  |
| [latex]-5[/latex] | |
| [latex]-8-\left(-3\right)=-5[/latex] |
try it
Model each subtraction. 1. [latex]7 - (-8)[/latex] 2. [latex]-2 - (-2)[/latex] 3. [latex]4 - 1[/latex] 4. [latex]-6 - 8[/latex]Answer:
1.
 2.
2.
 3.
3.
 4.
4.

Answer:
1.
 2.
2.
 3.
3.
 4.
4.

example
Model each subtraction expression:- [latex]2 - 8[/latex]
- [latex]-3-\left(-8\right)[/latex]
Answer: Solution
| 1. We start with [latex]2[/latex] positives. |  |
| We need to take away [latex]8[/latex] positives, but we have only [latex]2[/latex]. | |
| Add neutral pairs until there are [latex]8[/latex] positives to take away. |  |
| Then take away [latex]8[/latex] positives. |  |
| Find the number of counters that are left. There are [latex]6[/latex] negatives. |  |
| [latex]2 - 8=-6[/latex] |
| 2. We start with [latex]3[/latex] negatives. |  |
| We need to take away [latex]8[/latex] negatives, but we have only [latex]3[/latex]. | |
| Add neutral pairs until there are [latex]8[/latex] negatives to take away. |  |
| Then take away the [latex]8[/latex] negatives. |  |
| Find the number of counters that are left. There are [latex]5[/latex] positives. |  |
| [latex]-3-\left(-8\right)=5[/latex] |
try it
Model each subtraction expression.- [latex]7 - 9[/latex]
- [latex]-5--9[/latex]
Answer:
1.
 [latex-display]−2[/latex-display]
2.
[latex-display]−2[/latex-display]
2.
 [latex-display]4[/latex-display]
[latex-display]4[/latex-display]
- [latex]4 - 7[/latex]
- [latex]-7-\left(-10\right)[/latex]
Answer:
1.
 [latex-display]−3[/latex-display]
2.
[latex-display]−3[/latex-display]
2.
 [latex-display]3[/latex-display]
[latex-display]3[/latex-display]
Licenses & Attributions
CC licensed content, Shared previously
- Subtracting Integers with Color Counters (No Extra Zeros Needed). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
