Solutions for Polar Coordinates
Solutions to Try Its
1.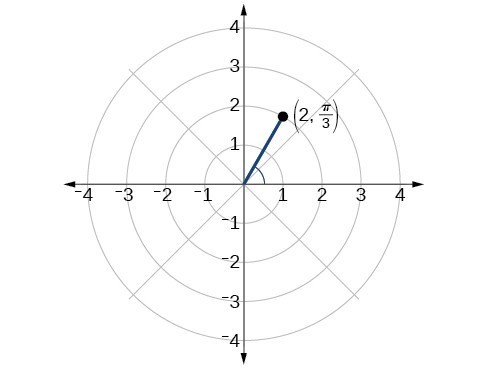 2.
2.
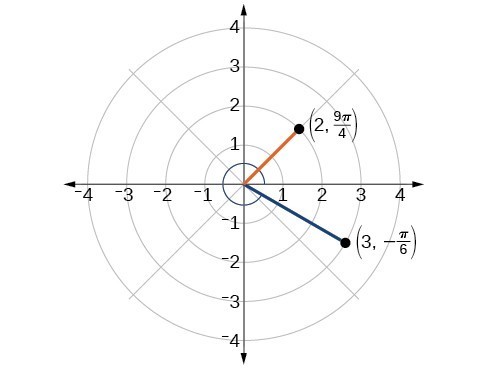 3. [latex]\left(x,y\right)=\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)[/latex]
4. [latex]r=\sqrt{3}[/latex]
5. [latex]{x}^{2}+{y}^{2}=2y[/latex] or, in the standard form for a circle, [latex]{x}^{2}+{\left(y - 1\right)}^{2}=1[/latex]
3. [latex]\left(x,y\right)=\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)[/latex]
4. [latex]r=\sqrt{3}[/latex]
5. [latex]{x}^{2}+{y}^{2}=2y[/latex] or, in the standard form for a circle, [latex]{x}^{2}+{\left(y - 1\right)}^{2}=1[/latex]
Solutions to Odd-Numbered Exercises
1. For polar coordinates, the point in the plane depends on the angle from the positive x-axis and distance from the origin, while in Cartesian coordinates, the point represents the horizontal and vertical distances from the origin. For each point in the coordinate plane, there is one representation, but for each point in the polar plane, there are infinite representations. 3. Determine [latex]\theta [/latex] for the point, then move [latex]r[/latex] units from the pole to plot the point. If [latex]r[/latex] is negative, move [latex]r[/latex] units from the pole in the opposite direction but along the same angle. The point is a distance of [latex]r[/latex] away from the origin at an angle of [latex]\theta [/latex] from the polar axis. 5. The point [latex]\left(-3,\frac{\pi }{2}\right)[/latex] has a positive angle but a negative radius and is plotted by moving to an angle of [latex]\frac{\pi }{2}[/latex] and then moving 3 units in the negative direction. This places the point 3 units down the negative y-axis. The point [latex]\left(3,-\frac{\pi }{2}\right)[/latex] has a negative angle and a positive radius and is plotted by first moving to an angle of [latex]-\frac{\pi }{2}[/latex] and then moving 3 units down, which is the positive direction for a negative angle. The point is also 3 units down the negative y-axis. 7. [latex]\left(-5,0\right)[/latex] 9. [latex]\left(-\frac{3\sqrt{3}}{2},-\frac{3}{2}\right)[/latex] 11. [latex]\left(2\sqrt{5}, 0.464\right)[/latex] 13. [latex]\left(\sqrt{34},5.253\right)[/latex] 15. [latex]\left(8\sqrt{2},\frac{\pi }{4}\right)[/latex] 17. [latex]r=4\csc \theta [/latex] 19. [latex]r=\sqrt[3]{\frac{sin\theta }{2co{s}^{4}\theta }}[/latex] 21. [latex]r=3\cos \theta [/latex] 23. [latex]r=\frac{3\sin \theta }{\cos \left(2\theta \right)}[/latex] 25. [latex]r=\frac{9\sin \theta }{{\cos }^{2}\theta }[/latex] 27. [latex]r=\sqrt{\frac{1}{9\cos \theta \sin \theta }}[/latex] 29. [latex]{x}^{2}+{y}^{2}=4x[/latex] or [latex]\frac{{\left(x - 2\right)}^{2}}{4}+\frac{{y}^{2}}{4}=1[/latex]; circle 31. [latex]3y+x=6[/latex]; line 33. [latex]y=3[/latex]; line 35. [latex]xy=4[/latex]; hyperbola 37. [latex]{x}^{2}+{y}^{2}=4[/latex]; circle 39. [latex]x - 5y=3[/latex]; line 41. [latex]\left(3,\frac{3\pi }{4}\right)[/latex] 43. [latex]\left(5,\pi \right)[/latex] 45.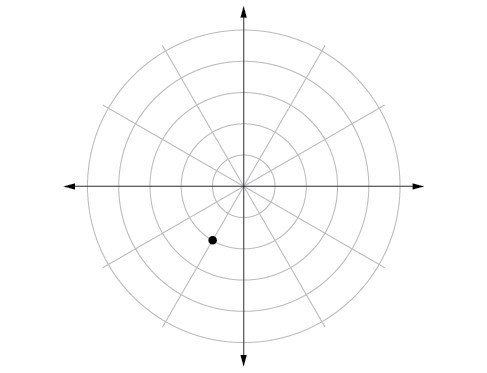 47.
47.
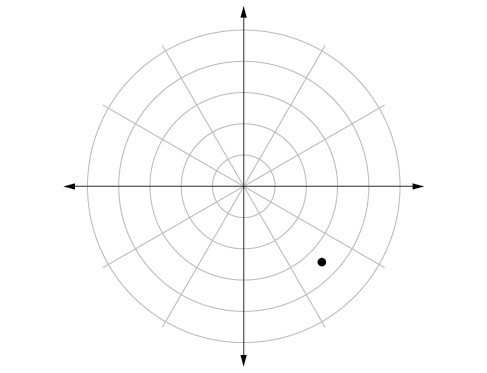 49.
49.
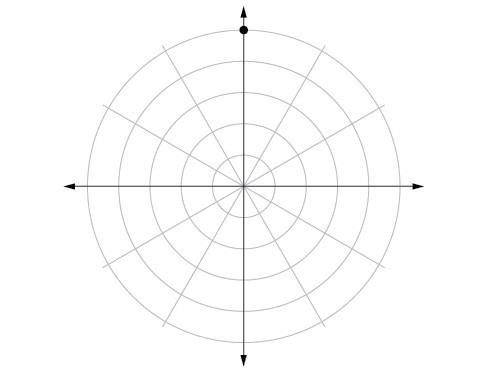 51.
51.
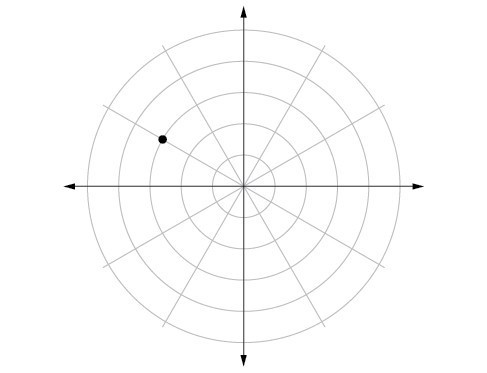 53.
53.
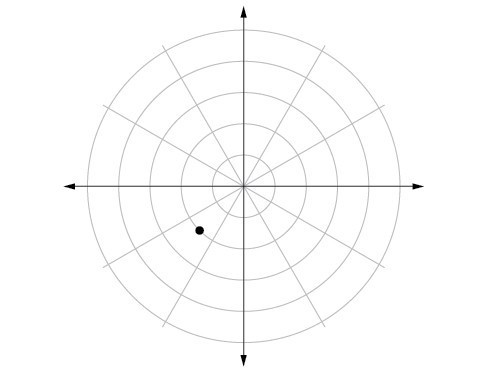 55. [latex]r=\frac{6}{5\cos \theta -\sin \theta }[/latex]
55. [latex]r=\frac{6}{5\cos \theta -\sin \theta }[/latex]
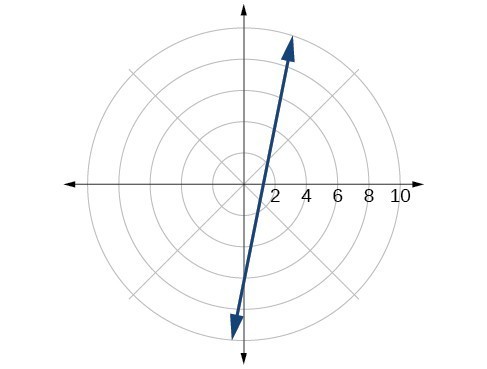 57. [latex]r=2\sin \theta [/latex]
57. [latex]r=2\sin \theta [/latex]
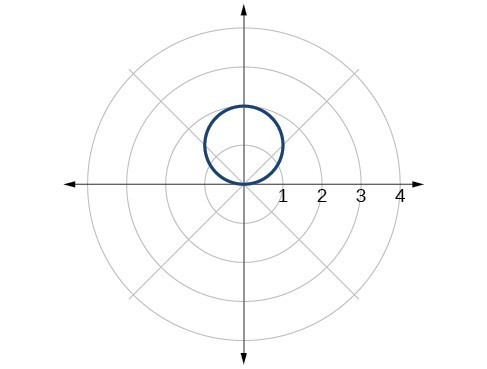 59. [latex]r=\frac{2}{\cos \theta }[/latex]
59. [latex]r=\frac{2}{\cos \theta }[/latex]
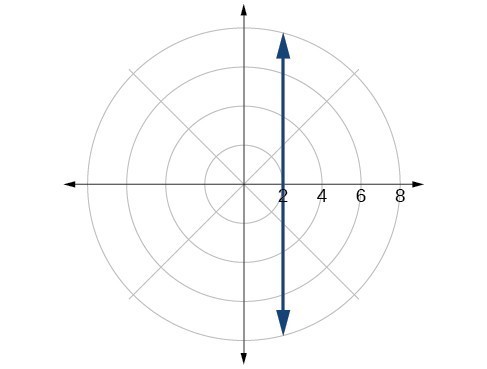 61. [latex]r=3\cos \theta [/latex]
61. [latex]r=3\cos \theta [/latex]
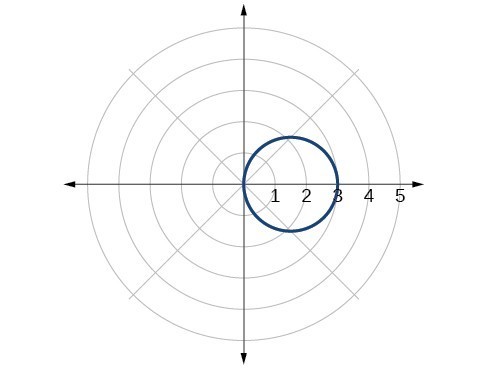 63. [latex]{x}^{2}+{y}^{2}=16[/latex]
63. [latex]{x}^{2}+{y}^{2}=16[/latex]
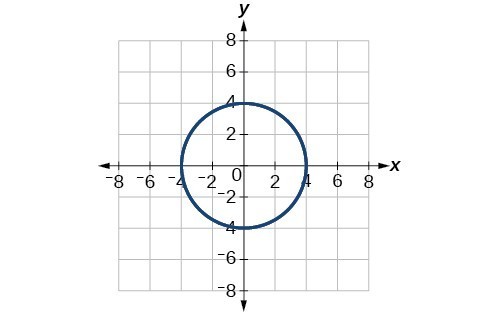 65. [latex]y=x[/latex]
65. [latex]y=x[/latex]
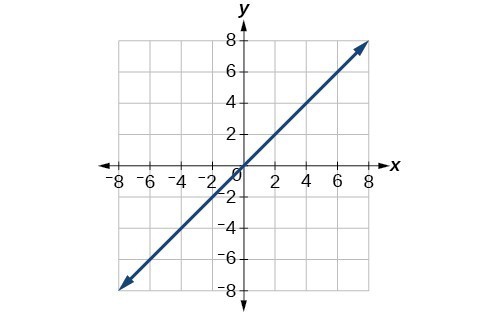 67. [latex]{x}^{2}+{\left(y+5\right)}^{2}=25[/latex]
67. [latex]{x}^{2}+{\left(y+5\right)}^{2}=25[/latex]
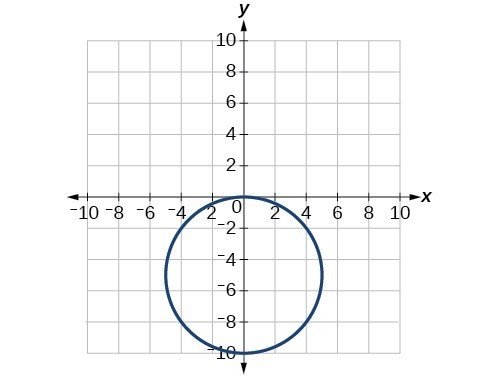 69. [latex]\left(1.618,-1.176\right)[/latex]
71. [latex]\left(10.630,131.186^\circ \right)[/latex]
73. [latex]\left(2,3.14\right)or\left(2,\pi \right)[/latex]
75. A vertical line with [latex]a[/latex] units left of the y-axis.
77. A horizontal line with [latex]a[/latex] units below the x-axis.
79.
69. [latex]\left(1.618,-1.176\right)[/latex]
71. [latex]\left(10.630,131.186^\circ \right)[/latex]
73. [latex]\left(2,3.14\right)or\left(2,\pi \right)[/latex]
75. A vertical line with [latex]a[/latex] units left of the y-axis.
77. A horizontal line with [latex]a[/latex] units below the x-axis.
79.
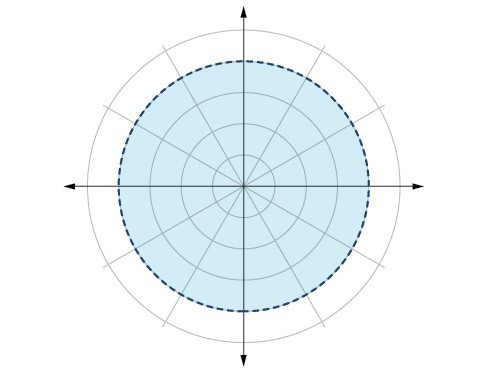 81.
81.
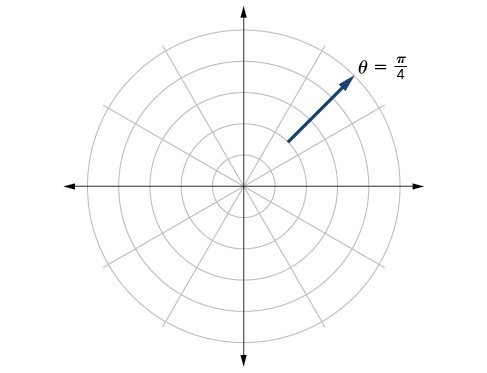 83.
83.
Licenses & Attributions
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
