Solutions for Parametric Equations: Graphs
Solutions to Try Its
1. 2.
2.
 3. The graph of the parametric equations is in red and the graph of the rectangular equation is drawn in blue dots on top of the parametric equations.
3. The graph of the parametric equations is in red and the graph of the rectangular equation is drawn in blue dots on top of the parametric equations.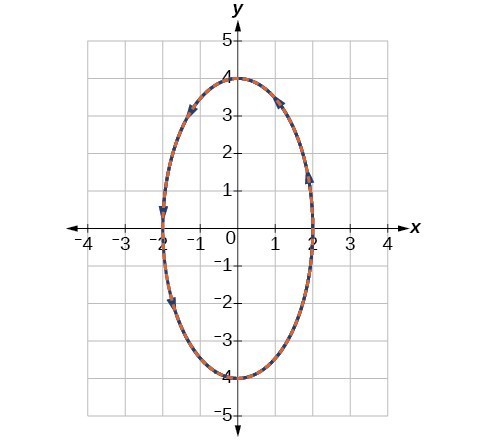
Solutions to Odd-Numbered Exercises
1. plotting points with the orientation arrow and a graphing calculator 3. The arrows show the orientation, the direction of motion according to increasing values of [latex]t[/latex]. 5. The parametric equations show the different vertical and horizontal motions over time. 7. 9.
9.
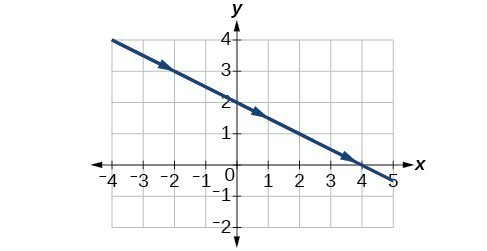 11.
11.
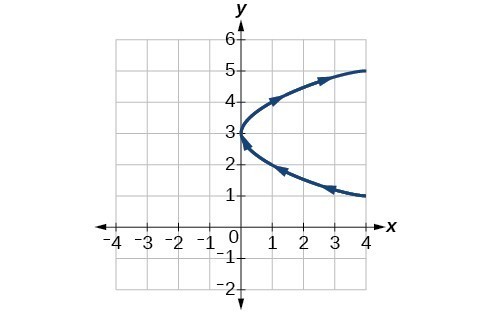 13.
13.
 15.
15.
 17.
17.
 19.
19.
 21.
21.
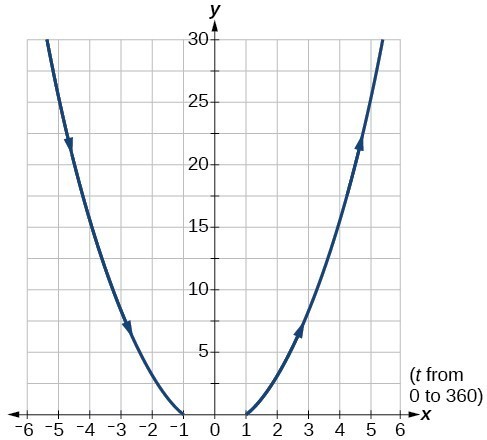 23.
23.
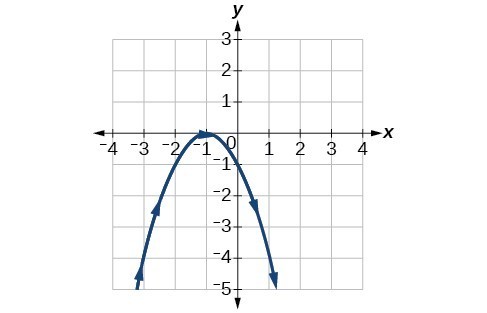 25.
25.
 27.
27.
 29.
29.
 31.
31.
 33.
33.
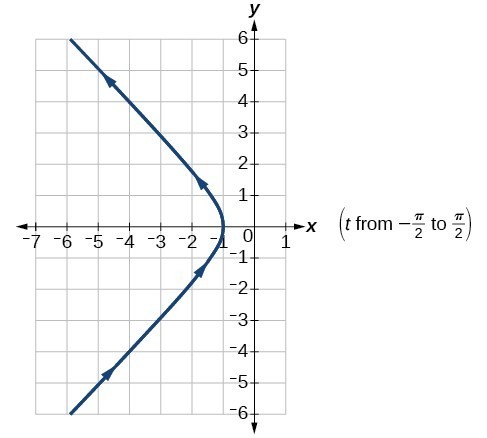 35.
35.
 37.
37.
 39. There will be 100 back-and-forth motions.
41. Take the opposite of the [latex]x\left(t\right)[/latex] equation.
43. The parabola opens up.
45. [latex]\begin{cases}x\left(t\right)=5\cos t\\ y\left(t\right)=5\sin t\end{cases}[/latex]
47.
39. There will be 100 back-and-forth motions.
41. Take the opposite of the [latex]x\left(t\right)[/latex] equation.
43. The parabola opens up.
45. [latex]\begin{cases}x\left(t\right)=5\cos t\\ y\left(t\right)=5\sin t\end{cases}[/latex]
47.
 49.
49.
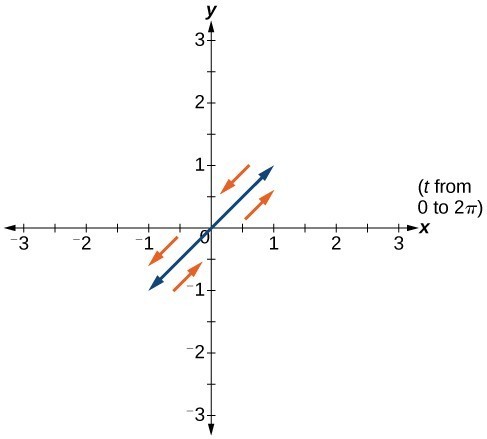 51.
51.
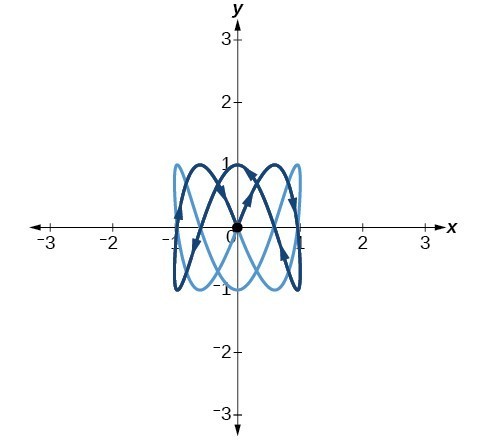 53. [latex]a=4,b=3,c=6,d=1[/latex]
55. [latex]a=4,b=2,c=3,d=3[/latex]
57.
53. [latex]a=4,b=3,c=6,d=1[/latex]
55. [latex]a=4,b=2,c=3,d=3[/latex]
57.
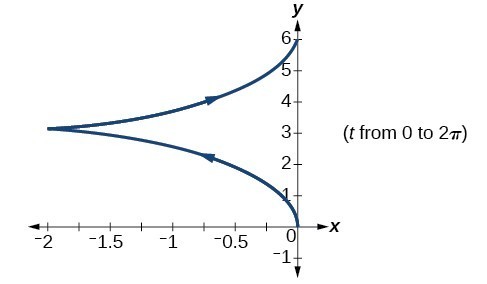

 59.
59.
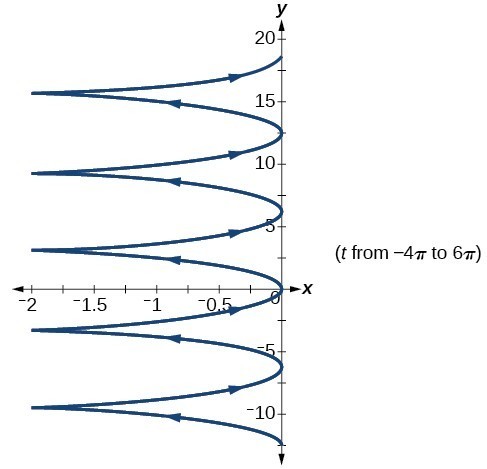

 61. The [latex]y[/latex] -intercept changes.
63. [latex]y\left(x\right)=-16{\left(\frac{x}{15}\right)}^{2}+20\left(\frac{x}{15}\right)[/latex]
65. [latex]\begin{cases}x\left(t\right)=64t\cos \left(52^\circ \right)\\ y\left(t\right)=-16{t}^{2}+64t\sin \left(52^\circ \right)\end{cases}[/latex]
67. approximately 3.2 seconds
69. 1.6 seconds
71.
61. The [latex]y[/latex] -intercept changes.
63. [latex]y\left(x\right)=-16{\left(\frac{x}{15}\right)}^{2}+20\left(\frac{x}{15}\right)[/latex]
65. [latex]\begin{cases}x\left(t\right)=64t\cos \left(52^\circ \right)\\ y\left(t\right)=-16{t}^{2}+64t\sin \left(52^\circ \right)\end{cases}[/latex]
67. approximately 3.2 seconds
69. 1.6 seconds
71.
 73.
73.

Licenses & Attributions
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
